This is an old revision of the document!
More on Interpretations. Herbrand Theorem
In this continuation of lecture09, we discuss the foundations behind automated theorem provers for first-order logic. We describe a procedure that, given enough time, will prove any valid formula of first-order logic.
More on Interpretations
Decision Problem for Validity in First-Order Logic
Normal Forms for First-Order Logic
Preliminary Discussion on Models
Difficulty in checking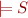 
: there are infinitely many models, of arbitrarily large cardinalities.
Goal: show that if a set 
of formulas has a model, then it has a model of particular sort. Then it suffices to look into those models.
Semidecision Procedure for First-Order Logic without Equality
Undecidability of First-Order Logic
Theorems on Cardinalities of Models