Complete Recursive Axiomatizations
Theorem: Let a set of first-order sentences  be a recursively enumerable axiomatization for a complete and consistent theory, that is:
be a recursively enumerable axiomatization for a complete and consistent theory, that is:
 is recursively enumerable: there exists an enumerateion
is recursively enumerable: there exists an enumerateion 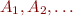 of the set
of the set  and there exists an algorithm that given
and there exists an algorithm that given  computes
computes  ;
; is complete: for each FOL sentence
is complete: for each FOL sentence  , either
, either  or
or 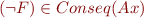 ;
;
Then there exists an algorithm for checking, given  , whether
, whether  .
.
Proof.
In short: if a complete theory has a recursively enumerable axiomatization, then this theory is decidable.
Conversely: if a theory is undecidable (there is no algorithm for deciding whether a sentence is true or false), then the theory does not have a recursive axiomatization.
Note:
- a finite axiomatization is recursively enumerable
- typical axiomatizations that use “axiom schemas” are also recursively enumerable
- if
 is an axiomatization for for some interpretation
is an axiomatization for for some interpretation  , that is
, that is 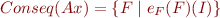 , then
, then  is an axiomatization of a complete theory
is an axiomatization of a complete theory
Corrollary: Let  be an interpretation. Then exactly one of the following is true:
be an interpretation. Then exactly one of the following is true:
- there exists an algorithm for checking
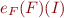
- there is no enumerable set of axioms
 such that
such that  .
.
Example: the theory of integers with multiplication and quantifiers is undecidable
- consequently, there are no complete axiomatizations for it, no decidable set of axioms from which the truth value of facts about natural numbers follows
- this result is one part of Goedel's incompleteness theorem
 ; the procedure terminates if any of these theorem provers succeed (the theorem provers simultaneously searches for longer and longer proofs from a larger and larger finite subsets of
; the procedure terminates if any of these theorem provers succeed (the theorem provers simultaneously searches for longer and longer proofs from a larger and larger finite subsets of 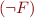 is proved, then by soundness of theorem prover
is proved, then by soundness of theorem prover  .
.