First-Order Theories
(Building on First-Order Logic Semantics.)
Definition: A first-order theory is a set  of first-order logic sentences.
of first-order logic sentences.
Definition: A theory  is consistent if it is satisfiable.
is consistent if it is satisfiable.
Definition: A theory  is complete if for every closed first-order formula
is complete if for every closed first-order formula  , either
, either  or
or 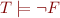 .
.
We have two main ways of defining theories: by taking a specific set of structures and looking at sentences true in these structures, or by looking at a set of axioms and looking at their consequences.
Definition: If  is a set of interpretations, then the theory of
is a set of interpretations, then the theory of  is the set of formulas that are true in all interepretations from
is the set of formulas that are true in all interepretations from  , that is
, that is 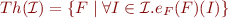 .
.
Note that 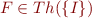 is equivalent to
is equivalent to 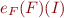 .
.
Lemma: For any interpretation  , the theory
, the theory 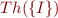 is complete.
is complete.
Definition (axiomatization of a theory): We say that  is an axiomatization of
is an axiomatization of  iff
iff 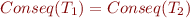 . Axiomatization
. Axiomatization  is finite if
is finite if  is a finite set. Axiomatization
is a finite set. Axiomatization  is recursive if it is a recursive set.
is recursive if it is a recursive set.
Example: Theory of Partial Orders
Consider the language 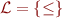 where
where  is a binary relation. Consider the following three sentences:
is a binary relation. Consider the following three sentences:
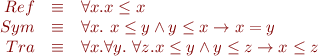
Let 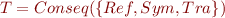 . Let us answer the following:
. Let us answer the following:
- Is
 consistent?
consistent? - Is
 complete?
complete?
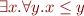 . It is true with the ordering on
. It is true with the ordering on  , but false with the ordering on
, but false with the ordering on  .
.