Recursive Set
We say that a set  is recursive (decidable) if there exists an algorithm that, given an element
is recursive (decidable) if there exists an algorithm that, given an element  determines whether
determines whether 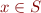 .
.
Example: the set of even numbers is recursive. The algorithm takes  represented in binary and checks whether its least signifficant digit is 0.
represented in binary and checks whether its least signifficant digit is 0.
Example: the set of all pairs 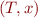 such that
such that  is a representation of Turing machine and
is a representation of Turing machine and  is an input such that
is an input such that  terminates on input
terminates on input  , is not recursive.
, is not recursive.
Example: the set of encodings of all valid first-order logic formulas is not recursive.
Example: the set of all valid formulas of Presburger arithmetic is recursive.