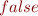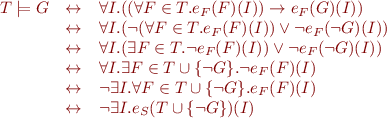First-Order Logic Semantics
(Recall First-Order Logic Syntax and Propositional Logic Semantics as well as Predicate Logic Informally.)
An interpretation for first-order logic language  is the pair
is the pair 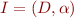 where
where  is a nonempty set, called the domain of interpretation, and
is a nonempty set, called the domain of interpretation, and  is the interpretation function, which assigns
is the interpretation function, which assigns
- to each first-order variable
 , an element
, an element 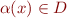
- to each relation symbol
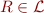 with arity
with arity 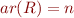 , a relation
, a relation 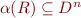
- to each function symbol
 with arity
with arity 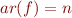 , a function
, a function 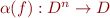
If 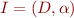 we denote
we denote  by
by  and
and  by
by  .
.
Because terms denote values from domain  and formulas denote truth values from
and formulas denote truth values from  , we define two semantic evaluation functions:
, we define two semantic evaluation functions:
We evaluate terms by recursion on the structure of  :
:
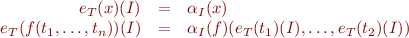
We evaluate formulas by recursion on the structure of  :
:
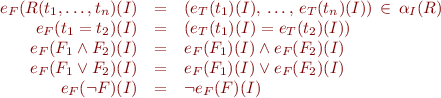
How do we evaluate quantifiers?
We generalize this notion as follows: if  is an interpretation and
is an interpretation and  is a set of first-order formulas, we write
is a set of first-order formulas, we write 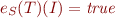 iff for every
iff for every 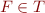 we have
we have 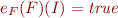 (set is treated as infinite conjunction). This is a generalization because
(set is treated as infinite conjunction). This is a generalization because 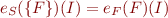 .
.
A terminological note: in algebra, an interpretation is often called a structure. Instead of using  mapping language
mapping language 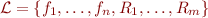 to interpretation of its symbols, the structure is denoted by a tuple
to interpretation of its symbols, the structure is denoted by a tuple 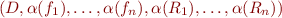 . For example, an interpretation with domain
. For example, an interpretation with domain  , with one binary operation whose interpretation is
, with one binary operation whose interpretation is  and one binary relation whose interpretation is
and one binary relation whose interpretation is  can be written as
can be written as  . This way we avoid writing
. This way we avoid writing  all the time, but it becomes more cumbersome to describe correspondence between structures.
all the time, but it becomes more cumbersome to describe correspondence between structures.
Examples
Example with Finite Domain
Consider language 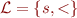 where
where  is a unary function symbol (
is a unary function symbol (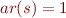 ) and
) and  is a binary relation symbol (
is a binary relation symbol ( ). Let
). Let 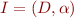 be given by
be given by
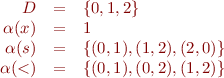
Let us evaluate the truth value of these formulas:
Example with Infinite Domain
Consider language 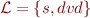 where
where  is a unary function symbol (
is a unary function symbol (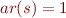 ) and
) and  is a binary relation symbol (
is a binary relation symbol (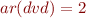 ). Let
). Let 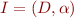 where
where 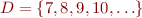 . Let
. Let  be defined as the “strictly divides” relation:
be defined as the “strictly divides” relation:
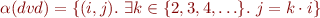
What is the truth value of this formula

What is the truth value of this formula
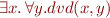
Domain Non-Emptiness
Let 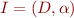 be an arbitrary interpretation. Consider formula
be an arbitrary interpretation. Consider formula

What is its truth value in  ? Which condition on definition of
? Which condition on definition of  did we use?
did we use?
This formula is true with the assumption that  is not empty.
is not empty.
With an empty domain, this formula would be false. There are other problems, for instance “how to evaluate a variable?”.
Satisfiability, Validity, and Semantic Consequence
Definition (satisfiability of set): If  is a set of formulas, a model of
is a set of formulas, a model of  is an interpretation such that
is an interpretation such that 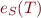 . A set
. A set  of first-order formulas is satisfiable if there exists a model for
of first-order formulas is satisfiable if there exists a model for  . A set
. A set  is unsatisfiable (contradictory) iff it is not satisfiable (it has no model).
is unsatisfiable (contradictory) iff it is not satisfiable (it has no model).
Note: taking 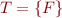 we obtain notion of satisfiability for formulas.
we obtain notion of satisfiability for formulas.
Definition (semantic consequence): We say that a set of formulas  is a semantic consequence of a set of formulas
is a semantic consequence of a set of formulas  and write
and write 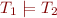 , iff every model of
, iff every model of  is also a model of
is also a model of  .
.
Definition: Formula is valid, denoted 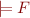 iff
iff  .
.
Lemma: 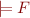 iff for every interpretation
iff for every interpretation  we have
we have 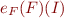 .
.
Lemma: A set  of formulas is unsatisfiable iff
of formulas is unsatisfiable iff 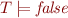 .
.
Lemma: Let  be a set of formulas and
be a set of formulas and  a formula. Then
a formula. Then 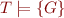 iff the set
iff the set 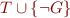 is contradictory.
is contradictory.
One of the central questions is the study of whether a set of formulas is contradictory, many basic questions reduce to this problem.
Consequence Set
Definition: The set of all consequences of  :
:
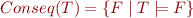
Note  is equivalent to
is equivalent to 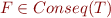 .
.
Lemma: The following properties hold:
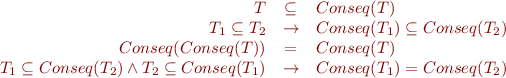


![Equation \begin{equation*}\begin{array}{rcl}
e_F(\exists x.F)((D_I,\alpha_I)) &=& (\exists d \in D_I.\ e_F(F)((D_I,\alpha_I[x \mapsto d])) \\
e_F(\forall x.F)((D_I,\alpha_I)) &=& (\forall d \in D_I.\ e_F(F)((D_I,\alpha_I[x \mapsto d]))
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgda39d1242fdea5902c52c384af7da18e.png)
![Math $\alpha_I[x \mapsto d]$](/w/lib/exe/fetch.php?media=wiki:latex:/imga8447d3e67debbe83b8f151406a364b6.png) .
.
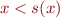
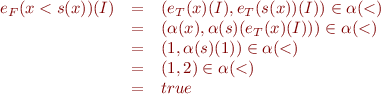
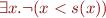
![Equation \begin{equation*}\begin{array}{rcl}
e_F(\exists x. \lnot (x < s(x)))(I) &=& (\exists d \in D.\ e_F(\lnot (x < s(x))(I[x \mapsto d]))\\
&=& \exists d \in D.\ \neg e_F((x < s(x))(I[x \mapsto d])\\
&=& \exists d \in D.\ (d, \alpha(s)(d)) \notin \alpha(<)\\
&=& (2,0)\notin \alpha(<)\\
&=& true
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img76d59a3c0edc62cf695a7f089c02860a.png)
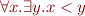
![Equation \begin{equation*}\begin{array}{rcl}
e_F(\forall x. \exists y. x < y)(I) &=& (\forall d \in D.\ e_F(\exists y. x < y)(I[x \mapsto d]))\\
&=& \forall d \in D.\ e_F(\exists y. x < y)(I[x \mapsto d])\\
&=& \forall d \in D.\ \exists e \in D. e_F(x < y)(I[x \mapsto d][y \mapsto e])\\
&=& \forall d \in D.\ \exists e \in D. (d,e) \in \alpha(<) \\
&=& \exists e \in D. (2,e) \in \alpha(<) \\
&=& ((2,0) \in \alpha(<)) \vee ((2,1) \in \alpha(<)) \vee ((2,2) \in \alpha(<))\\
&=& false
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img69ec1fc1951404f5fa488fa2d340654d.png)
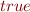 . For any
. For any  choose
choose  as
as 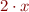 .
.