Sets and Relations
Sets
Sets are unordered collection of elements.
We denote a finite set containing only elements  ,
,  and
and  by
by 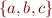 . The order and number of occurrences does not matter:
. The order and number of occurrences does not matter:
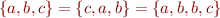 .
.
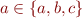
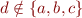 iff
iff 
Empty set:  . For every
. For every  we have
we have 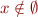 .
.
To denote large or infinite sets we can use set comprehensions: 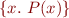 is set of all objects with property
is set of all objects with property  .
.
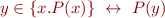
Notation for set comprehension: 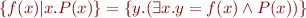
Sometimes the binder  can be inferred from context so we write simply
can be inferred from context so we write simply 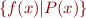 . In general there is ambiguity in which variables are bound. (Example: what does the
. In general there is ambiguity in which variables are bound. (Example: what does the  in
in  refer to in the expression:
refer to in the expression:
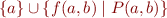
does it refer to the outerone  as in
as in  or is it a newly bound variable? The notation with dot and bar resolves this ambiguity.
or is it a newly bound variable? The notation with dot and bar resolves this ambiguity.
Subset:  means
means 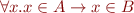
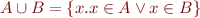
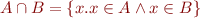
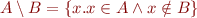
Boolean algebra of subsets of some set  (we define
(we define 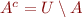 ):
):
 are associative, commutative, idempotent
are associative, commutative, idempotent- neutral and zero elements:
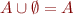 ,
, 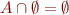
- absorption:
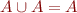 ,
, 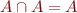
- deMorgan laws:
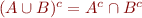 ,
, 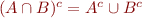
- complement as partition of universal set:
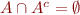 ,
, 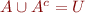
- double complement:
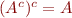
Which axioms are sufficient?
Infinte Unions and Intersections
Note that sets can be nested. Consider, for example, the following set 
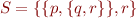
This set has two elements. The first element is another set. We have 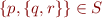 . Note that it is not the case that
. Note that it is not the case that
Suppose that we have a set  that contains other sets. We define union of the sets contained in
that contains other sets. We define union of the sets contained in  as follows:
as follows:
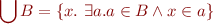
As a special case, we have
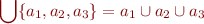
Often the elements of the set  are computed by a set comprehension of the form
are computed by a set comprehension of the form 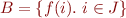 .
We then write
.
We then write
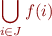
and the meaning is
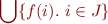
Therefore, 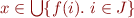 is equivalent to
is equivalent to  .
.
We analogously define intersection of elements in the set:
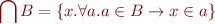
As a special case, we have
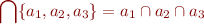
We similarly define intersection of an infinite family
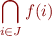
and the meaning is
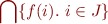
Therefore, 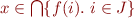 is equivalent to
is equivalent to  .
.
Relations
Pairs:

Cartesian product:

Relations  is simply a subset of
is simply a subset of  , that is
, that is 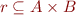 .
.
Note:
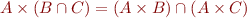
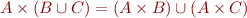
Diagonal relation
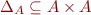 , is given by
, is given by
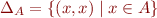
Set operations
Relations are sets of pairs, so operations 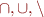 apply.
apply.
Relation Inverse

Relation Composition
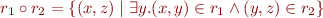
Note: relations on a set  together with relation composition and
together with relation composition and  form a monoid structure:
form a monoid structure:
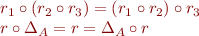
Moreover,
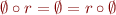

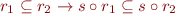
Relation Image
When  and
and 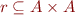 we define image of a set
we define image of a set  under relation
under relation  as
as
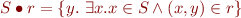
Transitive Closure
Iterated composition let 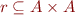 .
.
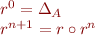
So,  is n-fold composition of relation with itself.
is n-fold composition of relation with itself.
Transitive closure:
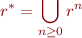
Equivalent statement: 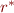 is equal to the least relation
is equal to the least relation  (with respect to
(with respect to  ) that satisfies
) that satisfies
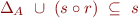
or, equivalently, the least relation  (with respect to
(with respect to  ) that satisfies
) that satisfies
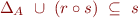
or, equivalently, the least relation  (with respect to
(with respect to  ) that satisfies
) that satisfies
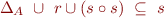
Some Laws in Algebra of Relations
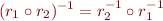
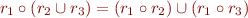
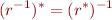
Binary relation 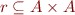 can be represented as a directed graph
can be represented as a directed graph 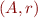 with nodes
with nodes  and edges
and edges 
- Graphical representation of
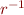 ,
, 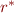 , and
, and 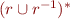
Equivalence relation  is relation with these properties:
is relation with these properties:
- reflexive:
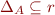
- symmetric:

- transitive:

Equivalence classes are defined by
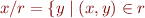
The set  is a partition:
is a partition:
- each set non-empty
- sets are disjoint
- their union is

Conversely: each collection of sets  that is a partition defines equivalence class by
that is a partition defines equivalence class by
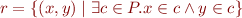
Congruence: equivalence that agrees with some set of operations.
Partial orders:
- reflexive
- antisymmetric:
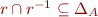
- transitive
Functions
Example: an example function 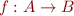 for
for 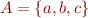 ,
, 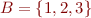 is
is
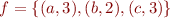
Definition of function, injectivity, surjectivity.
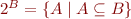
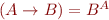 - the set of all functions from
- the set of all functions from  to
to  . For
. For  it is a strictly bigger set than
it is a strictly bigger set than  .
.
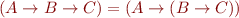 (think of exponentiation on numbers)
(think of exponentiation on numbers)
Note that  is isomorphic to
is isomorphic to 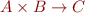 , they are two ways of representing functions with two arguments.
, they are two ways of representing functions with two arguments. 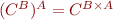
There is also isomorphism between
- n-tuples
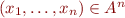 and
and - functions
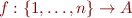 , where
, where 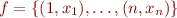
Function update
Function update operator takes a function 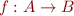 and two values
and two values  ,
,  and creates a new function
and creates a new function ![Math $f[a_0 \mapsto b_0]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgcac49089d0ce3df1d660788d24f4ca1e.png) that behaves like
that behaves like  in all points except at
in all points except at  , where it has value
, where it has value  . Formally,
. Formally,
 = \left\{\begin{array}{l}
b_0, \mbox{ if } x=a_0 \\
f(x), \mbox{ if } x \neq a_0
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgcfa989c8b9c0f4b0694d095cc6d3078f.png)
Domain and Range of Relations and Functions
For relation 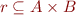 we define domain and range of
we define domain and range of  :
:
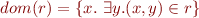
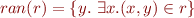
Clearly, 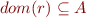 and
and 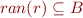 .
.
Partial Function
Notation: 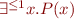 means
means 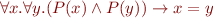 .
.
Partial function 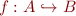 is relation
is relation 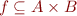 such that
such that
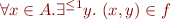
Generalization of function update is override of partial functions, 
Range, Image, and Composition
The following properties follow from the definitions:
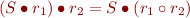
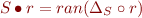
Further references
- Gallier Logic Book, Chapter 2