First-Order Logic
First-order logic is a very powerful notation that extends propositional logic. Here we give only an informal overview of first-order logic, which should be enough for you to understand the meaning of first-order logic formulas based on mathematics and natural language. In future lectures we study first-order logic as a formal system and discuss algorithmic questions in more detail.
On top of propositional operations, first-order logic adds:
- constructs to represent the structure of propositions:
- equality ( = )
- predicate symbols (
 ,
,  , …)
, …) - function symbols (
 ,
,  , …)
, …) - first-order variables (
 ,
,  , …) denoting entities in some domain
, …) denoting entities in some domain 
- quantifiers “forall” (
 ), “exists” (
), “exists” ( )
)
Uses of first-order logic
- precisely describe arbitrary mathematical statements (theorems, conjectures, properties)
- specify program properties
- represent the meaning of programs
- represent knowledge about the world (e.g. knowledge bases, semantic web)
Examples
- An ancestor of my ancestor is also my ancestor:
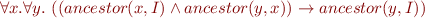
- Grandparent is the parent of a parent:

- Property
 holds for infinitely many natural numbers:
holds for infinitely many natural numbers: 
 is continuous in point
is continuous in point  :
: 
- first
 array elements are strictly positive, remaining elements are zero:
array elements are strictly positive, remaining elements are zero: 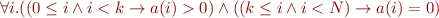
First-Order Logic Formulas
We build first-order logic formulas by starting from atomic formulas (defined below) and applying propositional operators and quantifiers:
- atomic formulas are first-order logic formulas
- if
 and
and  are first-order formulas, so are
are first-order formulas, so are  ,
, 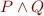 ,
,  ,
,  ,
, 
- if
 is a first-order formula, so is
is a first-order formula, so is  and
and 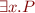
For a given value of variables, each formula evaluates to true or false. The rules for propositional operators are exactly as in propositional logic. Quantifiers can be seen as a way of generalizing conjunction and disjunction. First-order variables range over some domain  . In the special case of finite domain
. In the special case of finite domain 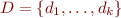 , we have that
, we have that
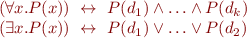
which corresponds to the intuitive definition of terms “for all” and “there exists”. Note, however, that  can be infinite in general (for example: the set of integers or reals).
can be infinite in general (for example: the set of integers or reals).
Atomic formulas evaluate to true or false. We build atomic formulas by applying predicate symbols and equality to terms:
- if
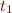 and
and  are terms, then
are terms, then 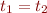 is an atomic formula;
is an atomic formula; - if
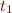 , …,
, …,  are terms and
are terms and  is a predicate symbol that takes
is a predicate symbol that takes  arguments, then
arguments, then 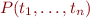 is an atomic formula.
is an atomic formula.
Predicates represent relations, for example, we can represent  as a binary relation.
as a binary relation.
Terms denote elements of the domain  . We build them starting from variables and constants and applying function symbols:
. We build them starting from variables and constants and applying function symbols:
- each first-order variable is a term
- a constant is a term
- if
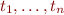 are terms and
are terms and  is a function symbol that takes
is a function symbol that takes  arguments, then
arguments, then  is also a term.
is also a term.
Example of constants are numerals for natural numbers, such as 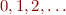 . Examples of function symbols are operations such as
. Examples of function symbols are operations such as 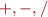 .
.
From above we see that the set of formulas depends on the set of predicate and function symbols. This set is is called vocabulary or language.
Bounded Quantifiers
In general all quantifiers range over some universal domain  . To restrict them to subsets of
. To restrict them to subsets of  , we can use bounded quantifiers:
, we can use bounded quantifiers:
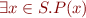 means
means 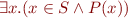
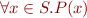 means
means 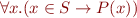 (note implication instead of conjunction)
(note implication instead of conjunction)
More generally, if  is some binary relation written in infix form, such as
is some binary relation written in infix form, such as 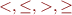 we write
we write
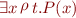 meaning
meaning 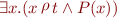
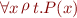 means
means  (note implication instead of conjunction)
(note implication instead of conjunction)
Evaluating First-Order Logic Formulas
To evaluate first-order logic formulas we need to know:
- the domain set

- values of first-order variables in the formula
- interpretation of predicate symbols and function symbols (e.g. does predicate symbol
 denote
denote  or
or  or
or  , does binary function symbol
, does binary function symbol  denote
denote  or
or  )
)
Examples
Consider formula  given by
given by  . The formula has one predicate symbol
. The formula has one predicate symbol  that takes one urgument (we call it unary) and one unary function symbol
that takes one urgument (we call it unary) and one unary function symbol  . Assume that the domain
. Assume that the domain  is the set of integers and consider two possible interpretations:
is the set of integers and consider two possible interpretations:
 denotes property of being an even integer and
denotes property of being an even integer and  denotes the successor function
denotes the successor function 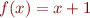 . Is formula true under this interpretation?
. Is formula true under this interpretation? denotes property of being an even integer and
denotes property of being an even integer and  denotes the squaring function
denotes the squaring function 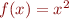 . Is formula true under this interpretation?
. Is formula true under this interpretation?
Now consider formula 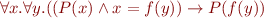 in each of these two interpretations.
in each of these two interpretations.
(Finite) Validity and Satisfiability of First-Order Logic Formulas
Formula is valid if and only if it evaluates to true for all domains, values of its variables and interpretations of predicate and function symbols.
Formula is satisfiable if and only if it evaluates to true for some domains, values of its variables, interpretation of predicate and function symbols.
Formula is unsatisfiable if and only if it is false for all domains, values of its variables and interpretations of predicate and function symbols.
Note
- a formula
 is unsatisfiable if and only if it is not satisfiable
is unsatisfiable if and only if it is not satisfiable - a formula
 is valid if and only if
is valid if and only if  is unsatisfiable
is unsatisfiable
Answers to some important algorithmic questions (not immediate):
- There is no algorithm that given a first-order logic formula outputs “yes” when the formula is valid and “no” otherwise - validity of first-order logic formulas is undecidable
- There exists an enumeration procedure that systematically lists all valid formulas (and only valid formulas) - validity of first-order logic formulas is enumerable
If instead of considering all domains we only consider finite domains (no natural numbers but only e.g. prefixes of natural numbers of the form 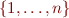 ) then we obtain notions of finite validity, finite satisfiability and finite unsatisfiability.
) then we obtain notions of finite validity, finite satisfiability and finite unsatisfiability.
Note that because finite domains are a special case of possible domains, we have the following:
- if a formula is finitely satisfiable, then it is satisfiable
- if a formula is valid, then it is also finitely valid
Answers to some important algorithmic questions about finite satisfiability:
- There is no algorithm that given a first-order logic formula outputs “yes” when the formula is satisfiable and “no” otherwise - finite satisfiability of first-order logic formulas is undecidable
- There exists an enumeration procedure that systematically lists all finitely satisfiable formulas (and only finitely satisfiable formulas) - finite satisfiability of first-order logic formulas is enumerable
Some Valid First-Order Logic Formulas
If we take a propositional tautology and replace equal propositional variables with equal atomic formulas, we obtain a valid formula. Such formula is called an instance of a tautology.
But there are many other valid formulas. Such formulas are valid laws of thinking that we often use in mathematics (explicitly, or implicitly without mentioning them).
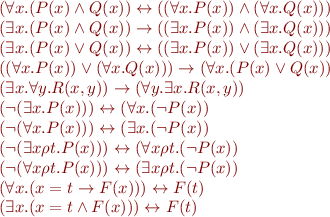
More information
- forthcoming lectures
- Calculus of Computation Textbook, Chapters 2, Chapter 3
- Gallier Logic Book, Sections 5.1, 5.2, 5.3