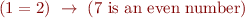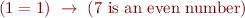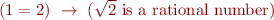LARA

Propositional Logic

Propositional logic is the core part of most logical formalisms (such as first-order and higher-order logic). It also describes well digital circuits that are the basis of most modern computing devices.

Importance of Propositional Logic

  • Many search problems can be encoded using propositional formulas
  • Checking equivalence of logical combinatorial circuits in hardware directly reduces to SAT
  • Can encode integer arithmetic with fixed bitwidth (e.g. operations on 16-bit integers)
  • An important class of logics can be obtained by giving meaning to propositional variables

Propositional Formulas

Propositional logic studies propositional formulas.

Propositional formulas are expressions built from

  • constants true and false
  • propositional variables, such as $p$, $q$, $p_1$, $q_1$, …
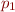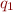  • logical operators ($\land, \lor, \lnot, \rightarrow, \leftrightarrow$) that combine propositional formulas into larger propositional formulas (we define their meaning below)

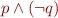Analogy with mathematical expressions: Just like a mathematical expression such as $2 \cdot x + 3 \cdot y$ specifies a binary function from values of $x$ and $y$ to the value $2x+3y$, a propositional formula such as $p \land (\lnot q)$ specifies a function from the values of $p$ and $q$ to the value $p \land (\lnot q)$.

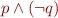Definitions of Logical Operations (Logical Connectives)

We specify a binary logical operation by a truth table: for each combination of arguments we indicate the result of the operation. For binary operation, the rows indicate the first argument, the columns indicate the second argument.

Negation (logical 'not')

\begin{equation*}\begin{array}{c|c} p & \lnot p \\\hline {\sl false} & {\sl true} \\ \hline {\sl true} & {\sl false} \end{array} \end{equation*}

Conjunction (logical 'and')

\begin{equation*}\begin{array}{c|cc} \land & {\sl false} & {\sl true} \\ \hline {\sl false} & {\sl false} & {\sl false} \\ \hline {\sl true} & {\sl false} & {\sl true} \end{array} \end{equation*}

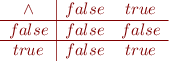
Disjunction (logical 'or')

\begin{equation*}\begin{array}{c|cc} \lor & {\sl false} & {\sl true} \\ \hline {\sl false} & {\sl false} & {\sl true} \\ \hline {\sl true} & {\sl true} & {\sl true} \end{array} \end{equation*}

Implication ('if')

\begin{equation*}\begin{array}{c|cc} \rightarrow & {\sl false} & {\sl true} \\ \hline {\sl false} & {\sl true} & {\sl true} \\ \hline {\sl true} & {\sl false} & {\sl true} \end{array} \end{equation*}

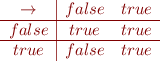
Check validity of these implications:

  • $(1=2)\ \rightarrow\ (7 \mbox{ is an even number})$
  • $(1=1)\ \rightarrow\ (7 \mbox{ is an even number})$
  • $(1=2)\ \rightarrow\ (\sqrt{2} \mbox{ is a rational number})$

Logical Eqivalence ('if and only if')

\begin{equation*}\begin{array}{c|cc} \leftrightarrow & {\sl false} & {\sl true} \\ \hline {\sl false} & {\sl true} & {\sl false} \\ \hline {\sl true} & {\sl false} & {\sl true} \end{array} \end{equation*}

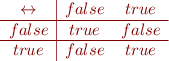
Evaluating Propositional Formulas

If we know values of variables in the formula, we can compute its value.

Let us evaluate formula

\begin{equation*} ((p \rightarrow q) \land\ ((\lnot p) \rightarrow r)) \leftrightarrow ((p \land q)\ \lor\ ((\lnot p) \land r)) \end{equation*}

for all values of its parameters. Let us draw formula as a tree. We introduce a column for each tree node. We obtain the value of a tree node by looking at the value of its children and applying the truth table for the operation in the node. The root gives the truth value of the formula.

Validity, Satisfiability of Logical Formulas

Formula is valid if it evaluates to true for all values of its variables (all columns for formula say true).

Formula is satisfiable if it evaluates to true for some values of its variables (true appears in at least one column).

Formula is unsatisfiable if it evaluates to false for all values of its variables (all columns for formula say false).

Observations

  • $F$ is unsatisfiable if and only if $F$ is not satisfiable
  • $F$ is valid if and only if $\lnot F$ is unsatisfiable

SAT problem: given a propositional formula $F$, check whether $F$ is satisfiable.

SAT is a well-known NP-complete problem.

Propositional Tautologies

Valid propositional formula is called propositional tautology, or tautology for short. Tautologies are basic principles of logical reasoning. They are true regardless of how complex the intended meaning of propositions is, as long as we are sure that each proposition evaluates to true or false.

Here is a small list of tautologies.

\begin{equation*}\begin{array}{l} (p \rightarrow q) \leftrightarrow ((\lnot p) \lor q) \\ (p \leftrightarrow q) \leftrightarrow ((p \rightarrow q) \land (q \rightarrow p)) \\ (p \land q) \leftrightarrow (q \land p) \\ (p \land (q \land r)) \leftrightarrow ((p \land q) \land r)) \\ (p \lor q) \leftrightarrow (q \lor p) \\ (p \lor (q \lor r)) \leftrightarrow ((p \lor q) \lor r)) \\ (p \land (q \lor r)) \leftrightarrow ((p \land q) \lor (p \land r)) \\ (p \lor (q \land r)) \leftrightarrow ((p \lor q) \land (p \lor r)) \\ \lnot (\lnot p) \leftrightarrow p \\ p \lor (\lnot p) \\ \lnot (p \land q) \leftrightarrow (\lnot p) \lor (\lnot q) \\ \lnot (p \lor q) \leftrightarrow (\lnot p) \land (\lnot q) \\ (p \rightarrow (q \rightarrow r)) \leftrightarrow ((p \land q) \rightarrow r) \\ (p \rightarrow (q \land r)) \leftrightarrow ((p \rightarrow q) \land (p \rightarrow r)) \\ ((p \lor q) \rightarrow r) \leftrightarrow ((p \rightarrow r) \land (q \rightarrow r)) \\ ((p \rightarrow {\sl false}) \leftrightarrow (\lnot p) \end{array}\end{equation*}

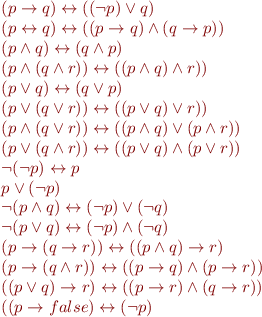
Suggest another tautology.

More information