First-Order Logic Syntax
(Compare to Propositional Logic Syntax.)
First order language  is a set of relation symbols
is a set of relation symbols  and function symbols
and function symbols  , each of which comes with arity
, each of which comes with arity 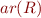 ,
,  , which are
, which are  . Function symbols of arity 0 are constants. Relation symbols of arity 0 are propositional variables.
. Function symbols of arity 0 are constants. Relation symbols of arity 0 are propositional variables.
The set  denotes countably infinite set of first-order variables, which is independent of the language.
denotes countably infinite set of first-order variables, which is independent of the language.
Terminology summary:
 - first-order logic formula (in language
- first-order logic formula (in language  )
) - atomic formula
- atomic formula - literals
- literals - term
- term - function symbol
- function symbol - relation symbol
- relation symbol - first-order variables
- first-order variables
Omitting parentheses:
 ,
,  are associative
are associative- priorities, from strongest-binding:
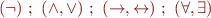
When in doubt, use parentheses.
Example: Consider language 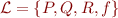 with
with 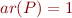 ,
, 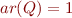 ,
, 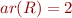 ,
, 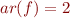 . Then
. Then
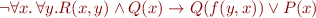
denotes
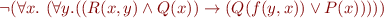
Often we use infix notation for relation and function symbols. In the example above, if we write  and
and  in infix notation, the formula becomes
in infix notation, the formula becomes
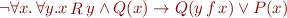
Notation: when we write  this means that
this means that  and
and  are identical formulas (with identical syntax trees). For example,
are identical formulas (with identical syntax trees). For example,  , but it is not the case that
, but it is not the case that  .
.
In Isabelle theorem prover we use this
ASCII notation for First-Order Logic
Usually we treat formulas as syntax trees and not strings.
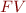 denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
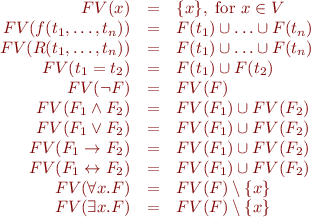
If 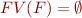 , we call
, we call  a closed first-order logic formula, or sentence.
a closed first-order logic formula, or sentence.
