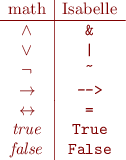Propositional Logic Syntax
Let  be a countable set of propositional variables, denoted by non-terminal V. The context-free grammar of propositional logic formulas
be a countable set of propositional variables, denoted by non-terminal V. The context-free grammar of propositional logic formulas  is the following:
is the following:
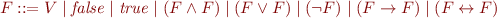
We denote the set of all propositional formulas given by the above context-free grammar by  . Each propositional formula is a finite sequence of symbols, given by the above context-free grammar. The set
. Each propositional formula is a finite sequence of symbols, given by the above context-free grammar. The set  is a countable set: we can order all formulas in this set in a sequence (for example, by writing them down in binary alphabet and sorting the resulting strings alphabetically).
is a countable set: we can order all formulas in this set in a sequence (for example, by writing them down in binary alphabet and sorting the resulting strings alphabetically).
Omitting parentheses:
 ,
,  associative
associative- priorities, from strongest-binding:
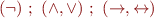
When in doubt, use parentheses.
Notation: when we write  this means that
this means that  and
and  are identical formulas (with identical syntax trees). For example,
are identical formulas (with identical syntax trees). For example,  , but it is not the case that
, but it is not the case that  .
.
In Isabelle theorem prover we use this
ASCII notation for Propositional Logic
Usually we work with syntax trees, as in Problem 3 in Homework 1.
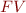 denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
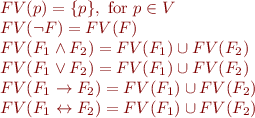
If 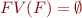 , we call
, we call  a ground formula.
a ground formula.