Cardinalities of Sets

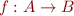Definition: We say that two sets $A$ , $B$ have same cardinality if there exists some bijective function $f : A \to B$ . Having same cardinality is a relationship between sets that has properties of equivalence relation.

Definition: For non-negative natural number $n$ we say that $A$ has cardinality $n$ if $A$ has same cardinality as $\{1,2,\ldots,n\}$ . The only set with cardinality zero is the empty set $\emptyset$ .

Definition: A set if finite if it has cardinality $n$ for some natural number, otherwise it is infinite.

Observation: The set of all natural numbers is infinite.

Definition: A set is countably infinite if it has the same cardinality as the set of natural numbers. A set is countable if it is finite or countably infinite.

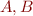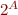Theorem: if $A, B$ are countable then $A \cup B$ and $A \times B$ are countable, but $2^A$ is not countable.

Observation: The set of all strings over some finite alphabet is countable.

Observation: The set of real numbers is not countable.

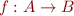Observation: If the set $A$ is infinite and the set $B$ has at least two elements, then set of all functions $f : A \to B$ is not countable.