Davis–Putnam algorithm (see Martin Davis, Martin Davis and Hilary Putnam)

Suppose has no model.

Then 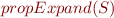has no model.

By propositional Compactness Theorem, some finite subset has no model.

Can check satisfiability of larger and larger initial prefixes of 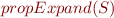using a SAT solver.

At some point we will reach a contradiction.

Semidecision procedure: if there exists a model, this procedure will loop forever.

• we cannot do much better in general: first-order logic is undecidable

(Some other logics do not even have semi-decision procedures.)