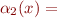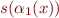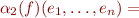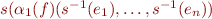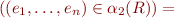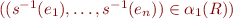Isomorphism of First-Order Logic Interpretations
(Building on First-Order Logic Semantics.)
Example: How many models does this formula have?
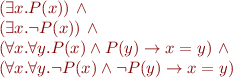
Informally, isomorphism is a function that establishes correspondence between two interpretations.
Definition:: An isomoprhism between 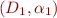 and
and 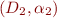 is a bijective function
is a bijective function  such that
such that
- for
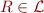 ,
, 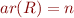 and all
and all 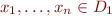
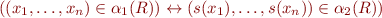
- for
 ,
, 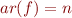 and all
and all 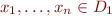
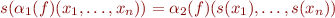
- for
 a first-order variable,
a first-order variable, 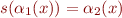 .
.
If 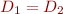 then the isomorphism
then the isomorphism  is called automorphism.
is called automorphism.
Definition: Interpretation 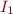 is isomorphic to interpretation
is isomorphic to interpretation 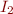 if there exists an isomorphism from
if there exists an isomorphism from 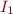 to
to 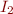 .
.
Note: the notion of graph isomorphisms is a special case of isomorphism of structures because we can view Graphs as Interpretations.
Lemma: Being isomorphic is reflexive, symmetric, and transitive property. Proof sketch:
End of Proof Sketch.
Lemma: If  is isomorphism from
is isomorphism from 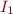 to
to 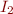 , then for every first-order term
, then for every first-order term  we have
we have
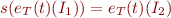
and for every first-order logic formula  we have
we have 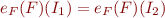 .
.
Proof:
Lemma: If 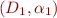 is an interpretation for language
is an interpretation for language  , if
, if  is a set and
is a set and  a bijective function, then there exists a mapping
a bijective function, then there exists a mapping  of symbols in
of symbols in  such that
such that 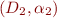 is an interpretation for
is an interpretation for  and
and 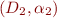 is isomorphic to
is isomorphic to 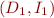 .
.
Proof: We construct  from
from  and
and  .
.
End of proof.
Corollary: Consider an interpretation 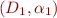 . If
. If  is finite, then there exists isomorphic interpretation
is finite, then there exists isomorphic interpretation 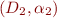 where
where 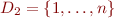 .
.
Also, note that for each permutation of 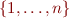 there is an automorphism that generates potentially a new interpretation. There are
there is an automorphism that generates potentially a new interpretation. There are 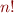 permutations.
permutations.
These observations are relevant for Finite-Model Finders.
 , let
, let 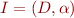 such that
such that 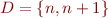 and
and 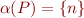 .
.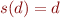 as the isomorphism
as the isomorphism
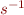
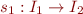 is isomorphism and
is isomorphism and 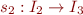 is isomorphism, then we claim
is isomorphism, then we claim 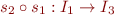 is isomorphism. Let us prove this for the case of function symbols:
is isomorphism. Let us prove this for the case of function symbols:
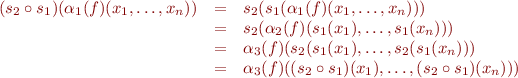
 .
.
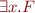 . Induction issues, function update on isomorphic interpretations.
. Induction issues, function update on isomorphic interpretations.