Consider formulas of first order logic (recall Predicate Logic Informally).

A model of is an interpretation in which is true.

We can define these notions precisely: First-Order Logic.

For a given bound , is there an interpretation of a given formula with a domain of size ?

This problem is decidable: consider domain 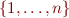. The number of all possible interpretations with this domain is finite.

Finite model finder: a tool that searches for such models.

Approaches:

• generalize SAT algorithms to search for finite domains and not just propositional ones (SEM)
• encoding into SAT (popular recently because SAT solvers are good): MACE, Paradox, KodKod (used in Alloy)

Issues when encoding into SAT:

• detecting sharing to minimizing size of propositional formula
• symmetry breaking - larger formula with fewer instances
• sort inference - smaller range of variables
• incremental search for different sizes of the domain - reusing work in SAT solver

Symmetry breaking among issues of encoding into SAT.

• Nitpick
• http://web.mit.edu/~emina/www/kodkod.html
• http://www.cs.chalmers.se/~koen/folkung/
• http://alloy.mit.edu