LARA

Intuition for 'Higher-Order' Logic

In first-order logic formulas contain

  • variables
  • function symbols
  • predicate symbols

First-order logic (FOL) is called 'first-order' because we can only quantify over variables, which are elements of the domain. We cannot quantify over interpretations of function symbols or relation symbols. In higher-order logic (HOL) we can quantify over functions and relations as well.

In FOL, we ask for satisfiability of a FOL formula, we are asking if there exist some interpretations of functions and relations for which formula evaluates to true. For example, formula

\begin{equation*} \forall x. \lnot R(x,f(x)) \end{equation*}

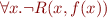
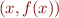is satisfiable iff there exist a relation interpreting $R$ and a function interpreting $f$ such that for all $x$ the pair $(x,f(x))$ does not belong to interpretation. Informally, we could therefore describe satisfiability of the above formula as

\begin{equation*} \exists R. \exists f. \forall x. \lnot R(x,f(x)) \end{equation*}

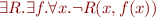
Dually, validity of the formula would correspond to the statement

\begin{equation*} \forall R. \forall f. \forall x. \lnot R(x,f(x)) \end{equation*}

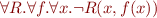
The last two formulas cannot be written in FOL, because they involve quantification over functions and relations. However, these formulas can be written in HOL. Moreover, in HOL we can write more complex conditions that cannot be described directly in terms of validity or satisfiability of FOL formulas, such as

\begin{equation*} \forall R. \exists f. \forall x. \lnot R(x,f(x)) \end{equation*}

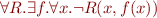
Clearly, there are differences between functions, relations, and individuals in terms of how we can use them. For example, predicates return truth values, whereas functions return values of the domain. HOL uses a type system, similar to one in programming languages, to ensure that we construct only sensible formulas.

Multisorted FOL

A related notion to FOL and HOL is multisorted FOL, which is a FOL where variables and terms have types. The most popular version has disjoint types, given by some set $B$ of types. These types are often called sorts. Each function symbol $f$ has arity, but the arity is not just a number, but a list of argument types and result types, that is, an expression of the form

\begin{equation*} \tau_1 \times \ldots \times \tau_n \to \tau_0 \end{equation*}

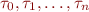where $\tau_0,\tau_1,\ldots,\tau_n$ are types. Similarly, each predicate symbol of $n$ arguments has a type of the form

\begin{equation*} \tau_1 \times \ldots \times \tau_n \end{equation*}

We build expressions using natural typing rules, allowing application only if the types match.

Interpretation of multisorted FOL, instead of having one domain $D$ has one domain $D_\tau$ for each type $\tau \in B$ and we typically require sets $D_\tau$ for different $\tau$ to be disjoint. Interpretation function $\alpha$ maps function symbol of arity $\tau_1 \times \ldots \times \tau_n \to \tau_0$ into a function

\begin{equation*} D_{\tau_1} \times \ldots \times D_{\tau_n} \to D_{\tau_0} \end{equation*}

and relation symbol of sort $\tau_1 \times \ldots \times \tau_n$ into a subset of

\begin{equation*} D_{\tau_1} \times \ldots \times D_{\tau_n} \end{equation*}

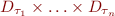
In multisorted FOL, we have disjoint countable sets of variables for each sort. We interpreted 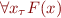$\forall x_\tau F(x)$ as bounded quantification $\forall d \in D_\tau. F(d)$.

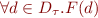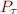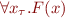Relation to standard FOL: Multisorted FOL can be represented as the standard FOL by using unary predicate $P_\tau$ for each sort $\tau$, adding axioms that these predicate interpretations are disjoint, and replacing quantification such as $\forall x_\tau. F(x)$ with bounded quantification

\begin{equation*} \forall x. P_\tau(x) \rightarrow F(x) \end{equation*}

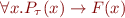
In multisorted logic with equality, we can introduce one binary equality symbol ${=}_\tau$ for each sort $\tau$, whose signature is $\tau \times \tau$.

In HOL we generalize the type system to have function types, and we use functions with different types to represent functions and predicates, allowing quantification over variables of arbitrary types. This starting point for such system is simply typed lambda calculus.