An example of a fixed point iteration not converging to a fixed point in one countable sequence
![Equation \begin{equation*}
\begin{array}{l}
f : [0,2] \to [0,2] \\begin{equation*}1ex]
f(x) = \left\{\begin{array}{rl}
\displaystyle\frac{1+x}{2}, & x < 1 \\begin{equation*}2ex]
\displaystyle \frac{3+2x}{4}, & x \geq 1 \end{array}\right.
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img9f82650b11328c1097a97888c8386833.png)
(draw figure)
Start from e.g. x=1/2. Obtain a series converging to 1, but 1 is not a fixed point because 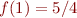 .
.
This is because  is not continuous. If it was continous (at least, continuous from the left), we would have the desired property.
is not continuous. If it was continous (at least, continuous from the left), we would have the desired property.
Whenever we converge to some  , we take
, we take 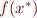 and continue iterating and taking limits (the “number of times” to iterate, even if infinite, depends on the size of the lattice, which can be formalized ordinal numbers).
and continue iterating and taking limits (the “number of times” to iterate, even if infinite, depends on the size of the lattice, which can be formalized ordinal numbers).