Graphs as Interpretations
Directed graph is given by a set of vertices  and a set of edges
and a set of edges 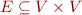 . Graph is therefore specified by an interpretation
. Graph is therefore specified by an interpretation 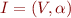 in languge
in languge 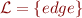 with
with 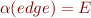 .
.
Example: 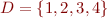 ,
, 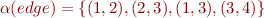 .
.
For a class of graph properties we can write down a formula  such that property holds for graph iff
such that property holds for graph iff  is true in the interpretation
is true in the interpretation  representing the graph.
representing the graph.
No self-loops:
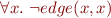
Undirected graph:
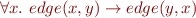
Tournament:

Note: there is no formula  in this language
in this language 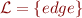 that characterizes property “graph has no cycles”. All properties expressed in first-order logic on graphs are “local”. Intuitively, formula with
that characterizes property “graph has no cycles”. All properties expressed in first-order logic on graphs are “local”. Intuitively, formula with  universal quantifiers says that if we pick any set of
universal quantifiers says that if we pick any set of  vertices in the graph, then they (and their close neighbors) can induce only one of the finitely many specified subgraphs.
vertices in the graph, then they (and their close neighbors) can induce only one of the finitely many specified subgraphs.
Many more properties become expressible if we take as domain  the set of all subsets of
the set of all subsets of  and allow set operations in our language.
and allow set operations in our language.