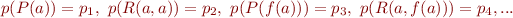Ground Terms as Domain of Interpretation
Recall syntax of first-order logic terms in First-Order Logic Syntax.
Ground term is a term  without variables, i.e.
without variables, i.e. 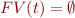 , i.e. given by grammar:
, i.e. given by grammar:
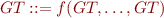
i.e. built from constants using function symbols.
Example
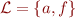
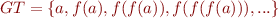
If  has no constants then
has no constants then  is empty. In that case, we add a fresh constant
is empty. In that case, we add a fresh constant  into the language and consider
into the language and consider 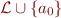 that has a non-empty
that has a non-empty  . We call the set
. We call the set  Herbrand Universe.
Herbrand Universe.
Goal: show that if a formula without equality (for now) has a model, then it has a model whose domain is Herbrand universe, that is, a model of the form 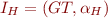 .
.
How to define 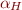 ?
?
Term Algebra Interpretation for Function Symbols
Let 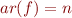 . Then
. Then 
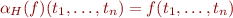
This defines 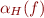 . How to define
. How to define 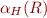 to ensure that elements of a set are true, i.e. that
to ensure that elements of a set are true, i.e. that  ?
?
Partition 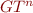 in two sets, one over which
in two sets, one over which 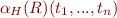 is true and the other over which it is false.
is true and the other over which it is false.
- is this possible for arbitrary set? no
Example
Consider a set that is not satisfiable : 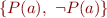
Ground Atoms
If 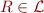 ,
, 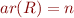 and
and 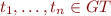 , we call
, we call 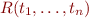 an Herbrand Atom. HA is the set of all Herbrand atoms:
an Herbrand Atom. HA is the set of all Herbrand atoms:
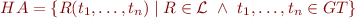
We order elements of  in sequence (e.g. sorted by length) and establish a bijection
in sequence (e.g. sorted by length) and establish a bijection  with propositional variables
with propositional variables
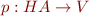
We will write 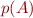 .
.
Example
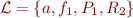
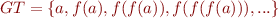
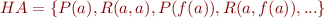
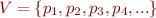
We define p such that :