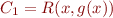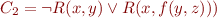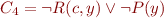Normal Forms for First-Order Logic
Example Formula
We will look at the language 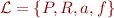 where
where
 is relation symbol of arity one
is relation symbol of arity one is relation symbol of arity two
is relation symbol of arity two is a constant
is a constant is a function symbol of two arguments
is a function symbol of two arguments
Consider this formula in  :
:
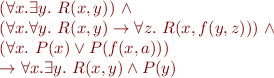
We are interested in checking the validity of this formula (is it true in all interpretations). We will check the satisfiability of the negation of this formula (does it have a model):
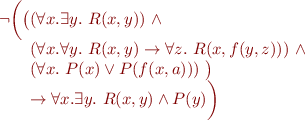
We will first consider a range of techniques that allow us to convert such formula to simpler normal forms.
Negation Normal Form
In negation normal form of formula the negation applies only to atomic formulas.
Every FOL formula can be transformed in NNF using the formulas used for the same purpose in PL extended by two new ones :
NNF of Example
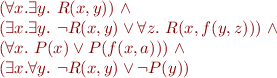
Prenex Normal Form
Prenex normal form has all quantifiers in front.
Prenex normal form (PNF) is a formula of the form
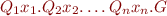
where 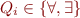 and
and  has no quantifiers.
has no quantifiers.
Any FOL formula can be transformed to PNF. First convert it to NNF, then if several quantified variables or free variables have the same name rename them to fresh names, and finaly use the following formulas :
PNF of Example
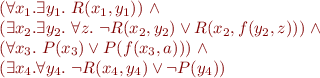
Skolem Normal Form
Let  be a predicate with two arguments.
be a predicate with two arguments.
Note that

but converse implication does not hold (take as  relation
relation  or
or  on natural numbers).
on natural numbers).
In general, we have this theorem:
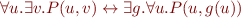
where  is a function.
is a function.
Proof:
( ): For each
): For each  we take
we take 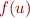 as the witness
as the witness  .
.
( ): We know there exists a witness
): We know there exists a witness  for each
for each  . We define
. We define  to map
to map  to one such witness
to one such witness  . (To prove that this is possible requires axiom of choice from set theory.)
. (To prove that this is possible requires axiom of choice from set theory.)
End Proof.
Note also that satisfiability of formula  expresses existential quantification over function symbols and relation symbols.
expresses existential quantification over function symbols and relation symbols.
Definition: Skolemization is the result of applying this transformation
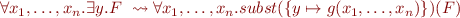
to the entire PNF formula to eliminate all existential quantifiers. Above,  is a fresh function symbol. Denote
is a fresh function symbol. Denote 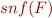 the result of applying skolemization to formula
the result of applying skolemization to formula  .
.
Lemma: A set of formulas  in prenex normal form is satisfiable iff the set
in prenex normal form is satisfiable iff the set 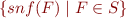 is satisfiable.
is satisfiable.
SNF for Example
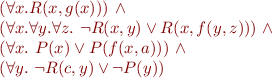
Note: it is better to do PNF and SNF for each conjunct independently.
CNF and Sets of Clauses
Let 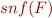 be
be  . Convert
. Convert  to conjunctive normal form
to conjunctive normal form  . Then
. Then 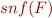 is equivalent to
is equivalent to
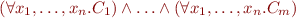
where each  is a disjunction of first-order literals. We call
is a disjunction of first-order literals. We call  (first-order) clause. For a given formula
(first-order) clause. For a given formula  , denote the set of such clauses in conjunctive normal form of
, denote the set of such clauses in conjunctive normal form of 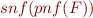 by
by 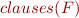 .
.
We omit universal quantifiers because all variables are universally quantified. We use a convention to denote variables by  and constants by
and constants by 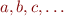 .
.
Theorem: The set  is satisfiable iff the set
is satisfiable iff the set

is satisfiable.
Clauses for Example
Another Example: Irreflexive Dense Linear Orders
Let 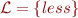 be binary relation (“strictly less”). We consider the following axioms for irreflexive partial order that is total and dense:
be binary relation (“strictly less”). We consider the following axioms for irreflexive partial order that is total and dense:
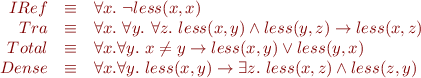
Let us find clauses for these axioms :
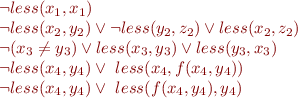







![Math $\neg \forall x.F[x] \Leftrightarrow \exists x. \neg F[x]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgacd5fb74825e35785c1641d0e54eea2a.png)
![Math $\neg \exists x.F[x] \Leftrightarrow \forall x. \neg F[x]$](/w/lib/exe/fetch.php?media=wiki:latex:/img747b4695336eb2273623031c7679ce0f.png)