Difficulty in semantic definition of validity and satisfiability: the definitions talk about arbitrary models (finite models, integers, real numbers, set theory, …)

If formula has a model of some size, it has many models of same size, from Isomorphism of Interpretations.

Are there first-order formulas that have only finite models?

Are there first-order formulas that have only infinite models?

What is the cardinality of the models we need to consider? There are many useful models whose domain is not a countable set (e.g. real numbers).

Difficulty in checking 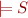: there are infinitely many models, of arbitrarily large cardinalities.

Goal: show that if a set of formulas has a model, then it has a particular kind of a model, and this model is countable.

• this will also give us a systematic method to search for unsatisfiable (and thus, for valid) formulas