Analysis of Assembly Execution Time
__________________________________________________________
/ _ _ _ _ ___ _ _ _ \
| | \| (_)__ ___| |__ _ ___ | _ ) ___(_)__| |_ __ _| |_ |
| | .` | / _/ _ \ / _` (_-< | _ \/ _ \ / _| ' \/ _` | _| |
| |_|\_|_\__\___/_\__,_/__/ |___/\___/_\__|_||_\__,_|\__| |
| |
| ___ _ ___ _ _ __ _ _ |
| | __|_ _(_)__ | _ |_)___ ___| |/ _|__ _| |_(_) |
| | _|| '_| / _| | _ \ (_-</ _ \ | _/ _` | _| | |
| |___|_| |_\__| |___/_/__/\___/_|_| \__,_|\__|_| |
\ /
----------------------------------------------------------
\ ^__^
\ (@@)\_______
(__)\ )\/\
U ||----w |
|| ||
Introduction
Execution time analysis can be very interesting when one wants to deduce properties on algorithms. For example, assume we have a cryptographic function that looks like the following:
int mult(int a, int b) {
int i, sum = 0;
for (i = 0; i < b; i++)
sum += a;
return sum;
}
In this function, the value of a is not really interesting, however, we see that the value of b can tremendously change the main loop, and thus, change the overall execution time. Moreover, if b is our cryptographic key, an attacker could deduce pretty easily its value just by recording the amount of time that was spent in the mult function.
This project is focusing on this kind of “leak of information”, and more specifically on preventing such leaks.
More formally, one can generally define an encryption function  as:
as:
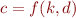
Where  is key being used (i.e. what we do not want to leak),
is key being used (i.e. what we do not want to leak),  is the data to
encode, that we can assume to be known or chosen by the attacker, and
is the data to
encode, that we can assume to be known or chosen by the attacker, and  is the
encrypted data (available to the attacker as well).
is the
encrypted data (available to the attacker as well).
For any given  , there is obviously a dependency between
, there is obviously a dependency between  and
and  , but we will not consider that here (we assume that the
encryption algorithm is sound and that
, but we will not consider that here (we assume that the
encryption algorithm is sound and that  is hard to find
given
is hard to find
given  and
and  ).
).
As a side effect of the encryption process, some time  will be spent to
execute the encryption algorithm.
We can then define the function
will be spent to
execute the encryption algorithm.
We can then define the function  :
:
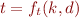
Our goal is, for any given  again, to check that there
is no dependency between the key
again, to check that there
is no dependency between the key  and
and  . More formally:
. More formally:
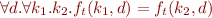
Implementation
To be able to analyse execution time, our tool has to work directly on the assembly code, for the 2 following reasons:
- Execution time depends on the assembly code only: It is clear that the same C function, compiled with 2 different compilers, or with different optimisation flags, will lead to different execution time.
- Each instruction execution time is known.
Architecture
To be able to do such an analysis, we restricted ourselves to a simple assembly instruction set. Analysing assembly code on, let's say, x86, is difficult, since the instruction set is large, the instructions themselves are not regular, the encoding is very complicated, and the microarchitecture of various generations of x86 CPUs varies greatly.
In order to simplify the problem, we chose to work on the FPGA4U board designed here at EPFL to simplify the problem. This board's Altera FPGA (Field-Programmable Gate Array) allows us to program a CPU on it. We selected the softcore NIOS II/e provided by Altera, because it is a simple multi-cycle processor (no pipelining), offering no cache, and the execution time is fully deterministic (provided the program memory is in Static RAM). On this processor, almost all instruction lasts 6 cycles, except for special instructions like shift operations or accesses to the memory Nios II specifications, page 21).
Thus, the first step was to write a disassembler able to understand the NIOS II assembly language (instruction format are explained in Nios II specifications, pages 43-143). From the elf file, we used “readelf” to get addresses of each of the functions in the program. From there, we were able to construct a control flow graph for the functions we are interested in.
Generating data flow dependencies from a control flow graph
Data dependencies
For each instruction, we have a map deps, indicating register dependencies.
Example:
add r2, r4, r5 -- deps: r2 -> (r4,r5) add r3, r2, r6 -- deps: r2 -> (r4,r5); r3 -> (r4,r5,r6)
This set can be formalized as follows:
First, define a set of registers other registers can depend on:
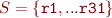
Note that, since functions have a limited number of parameters,  usually only contains a limited number of elements.
usually only contains a limited number of elements.
Then, we can note that the dependencies at each instructions are simply a list of sets of registers, which can be defined as:
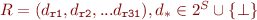
Note that  and
and  have different meaning here:
have different meaning here:  means that
the register has never been written, while
means that
the register has never been written, while  means the register depends
on nothing.
means the register depends
on nothing.
Dependencies are simply forwarded from all predecessors, then updated according to the operation done by the current instruction.
To perform this task, we are using the worklist algorithm presented in the course, which works as follow:
worklist = { control flow graph first node }
While (worklist not empty)
node = pick an element from worklist
olddeps = node.deps
node.deps = merge dependencies from node.predecessors (see below for the logic)
update node.deps depending on the current instruction (again, see below for the logic)
If olddeps != node.deps
worklist = worklist + node.successors
End While
Merging and update
Merging dependencies from predecessors is trivial, and is easily formalized as follows, if we assume there are  incoming branches to a node, with the following dependencies:
incoming branches to a node, with the following dependencies:
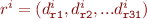
The merged dependencies are defined as follows:
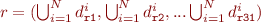
(for this purpose, we consider here 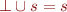 , this is
, this is  and
and  have the same behaviour).
have the same behaviour).
The update algorithm can be explained with a small example. Consider:
add r4, r0, r2
The new dependencies will be:
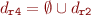 , if
, if 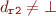
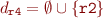 , if
, if 
Note that “r0” is a constant, so it does not depend on anything. Also, If  , it means
“r2” has never been modified before, which means it is a function parameter, and has to be put
in “r4” dependency list.
, it means
“r2” has never been modified before, which means it is a function parameter, and has to be put
in “r4” dependency list.
Lattice definition
To be able to verify that we are guaranteed to reach a convergence with this process, we will define formally the dependency maps.
A lattice on R can be easily defined as:
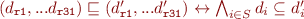
Since our update function 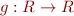 is monotonic (we only add register dependencies, and never remove any),
convergence is guaranteed due to Tarski's fixpoint theorem.
is monotonic (we only add register dependencies, and never remove any),
convergence is guaranteed due to Tarski's fixpoint theorem.
Branch dependencies
Using this, it is trivial to define, for each branch instruction, the registers on which the branch outcome depends.
Control flow and time dependencies
We have to take special care to handle branch instructions and their dependencies. They can typically introduce 2 types of dependencies:
- Control dependencies: the value of a register depends on the branch being taken
- Time dependencies: the execution time depends on the branch being taken
Both cases are important in our analysis. As a motivating example, we take this small code snippet:
int c = 0;
while (a > 0) {
if (b > 2) {
c += b-1;
} else {
c += b+1;
asm volatile( "nop" );
}
a--;
}
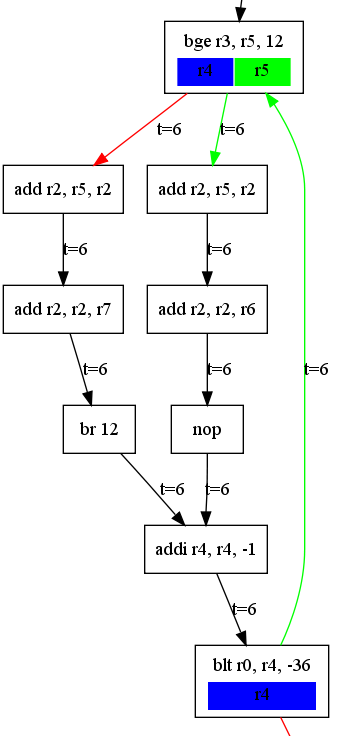
Graphically, this code translates to the following control flow graph:
When it comes to the first branch instruction (bge r3, r5, 12), it is clear time does not depend on which brand is taken. Indeed, following the green arrow will take a time of 24 cycles to reach a “merging point” (ie addi r4, r4, -1), which is the same as if the red arrow was followed. Thus, when a merging point is identified, and reached with the same time, we can say there are no time dependencies, if not, we can introduce a time dependency on r4 and r5 in this case.
Introducting the Post-Dominator algorithm
Dominators have applications in compilers for computing static single assignment form (SSA), but are also widely used for reverse engineering. This presentation gives a good insight of how dominators work.
We say that a node d dominates a node n if every path from the start node to n must go through d. By definition, every node dominates itself. In a similar way, we say that a node z post-dominates node n if after going through n, you always have to go through z. In our case, we are interested in post-dominator, given we are looking for merging points. The post-dominator algorithm is the same as the dominator algorithm, but with inverted arrows.
For our project, we used the trivial (and inefficient) iterative algorithm presented in Finding Dominators in Practice. Adapted for the post-dominator case, this works as follows:
We start by putting  , and compute the following on each other node
, and compute the following on each other node  :
:

The algorithm ends when there is no more change in the list of post-dominators.
Control flow dependencies
Control dependencies must also be handled. This means that if the execution of a given instruction depends on whether a branch is taken or not, the destination register of the instruction must also depend on the branch dependencies.
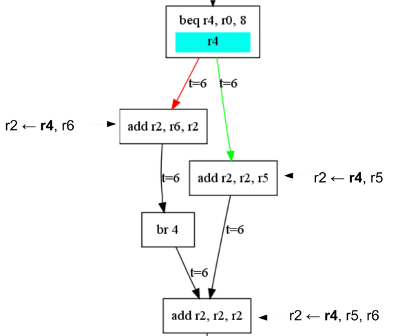
The picture below gives an example of such a control dependencies. The execution of instructions add r2, r6, r2 and add r2, r2, r5 is dependent on which branch is taken. Therefore, their destination register (r2) will depend on the branch condition (r4).
To obtain such behaviour, every time a branch is taken, we taint all the destination registers until we reach a post-dominator.
Note: This has another implication for the worklist algorithm above: every time branch dependencies are updated, we need to put all depending instructions in the worklist to make sure they are traversed again. Depending instruction are all successors which are not in the post-dominator of the branch instruction.
Time dependencies
Adding time dependencies in the propagation algorithm does not constitute a major problem. We just redefine the dependencies as:
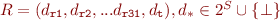
The time dependency  is forwarded the same way as the register dependencies.
is forwarded the same way as the register dependencies.
To be able to identify such dependencies, as soon as a branch operation is encountered, we record the time in both branches as we traverse the control flow graph. If, at any time, 2 branches merge with a different time, we add a time dependency corresponding to the branch dependencies.
If a branch introducing a time dependency is contained in another one, this logic will also report a time dependencies on the bigger branch operation.
Integration in the worklist algorithm
Control flow and time dependencies are easily integrated in the worklist algorithm. For this, every time a branch is encountered, we start a trace, which is forwarded in the control flow graph until a post-dominator of the branch instruction is encountered. Control flow dependencies can then be handled very easily: As long as a trace is active for a given branch, all instructions results are tainted by the branch dependencies.
To handle time dependencies, the trace also keeps track of the number of execution cycles consumed from the branch instruction. If, at any point, 2 traces from a given branch merge with a different time, we know we can add the branch dependencies to the time dependencies.
The updated algorithm can be given as follows:
worklist = { control flow graph first node }
While (worklist not empty)
node = pick an element from worklist
// Save old dependencies and traces
olddeps = node.deps
oldbrdeps = node.brdeps (branch dependencies)
oldtraces = node.traces
node.deps = merge dependencies from node.predecessors
update node.deps depending on the current instruction
node.traces = merge traces from node.predecessors
If any of the traces merge with different time
node.deps(time) += branch dependencies correspond to these traces
End If
remove node.traces for which node is in the post-dominators of the trace
update time in node.traces (according to current instruction)
If (node is conditional branch)
update node.brdeps for conditional branch instructions (logic similar to node.deps)
node.traces = node.traces + new trace(branch=node, time=0)
End If
If olddeps != node.deps OR oldtraces != node.traces OR oldbrdeps != node.brdeps
worklist = worklist + node.successors
End If
If oldbrdeps != node.brdeps (node is conditional branch)
// The branch dependencies were updated, so we need to go through all depending instructions
worklist = worklist + all nodes containing a trace starting in node
End If
End While
Stack and call handling
To be able to handle more complex application, we added support for call operations.
Call operations are trivial to handle. When such an instruction is encountered, the called function is analysed, and dependencies forwarded in the caller function. This simple behaviour does not allow to handle any kind of recursive functions, but support for those could be added with a little of work.
However, closely linked to call operation is stack operations. First, we need to know, for all instructions, the current stack pointer position. We can do that easily by using symbolic execution. We only allow 1 operation on the stack, namely an addi sp, sp, offset, where offset is a positive or negative number.
If, for any reason, the stack pointer is different on 2 predecessors of a given instruction, the tool will report the problem and fail.
Once the stack pointer position is known, we can also handle load and store operation in the form ldw rX, offset(sp) and stw rX, offset(sp). This increases the size of the set S, which we can now define as:

As mentioned before, only parameters of the function need to be in  (in Nios/II, a maximum of 4 parameters are passed through registers, the rest being pushed on the stack), so
(in Nios/II, a maximum of 4 parameters are passed through registers, the rest being pushed on the stack), so  is guaranteed to be finite.
is guaranteed to be finite.
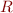 can then also be updated:
can then also be updated:
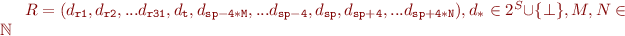
Since the stack pointer is only allow to move by a limited amount (this is guaranteed by the way our symbolic execution engine work),  has a finite number of elements and convergence is still guaranteed.
has a finite number of elements and convergence is still guaranteed.
This can be easily added to the worklist algorithm without adding much complexity.
Case study: Finite field multiplication function
As a case study, we will analyse a Finite field multiplication function that can be used in some cryptographic device:
/* Multiply two numbers in the GF(2^8) finite field defined
* by the polynomial x^8 + x^4 + x^3 + x + 1 */
uint8_t gmul(uint8_t a, uint8_t b) {
uint8_t p = 0;
uint8_t counter;
uint8_t hi_bit_set;
for(counter = 0; counter < 8; counter++) {
if((b & 1) == 1)
p ^= a;
hi_bit_set = (a & 0x80);
a <<= 1;
if(hi_bit_set == 0x80)
a ^= 0x1b; /* x^8 + x^4 + x^3 + x + 1 */
b >>= 1;
}
return p;
}
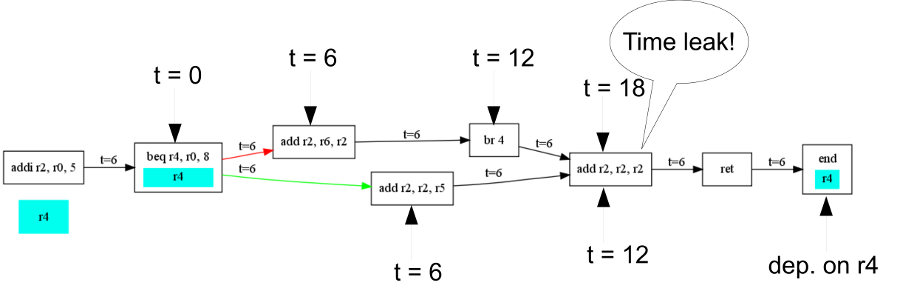
Running our analysis on this function would result in the following graph. Note that due to the calling convention of the Nios/II, a is passed in register r4, b in r5 and the return value is r2.
We will here assume that a contains some data (i.e. non-sensitive information), and that b contains the key. We then want to avoid time dependencies on b (i.e. r5). The analysis tool immediately reports that our function is not safe, since its execution time depends on a and b (r4 and r5, as indicated in the block named end).
This dependency is caused by the branch highlighted in red:
beq r2, r0, 4
Which causes the branch to be taken (i.e. the xor operation to be skipped) if r2 is not equal to zero. However, r2 directly depends on r5, because of the instruction highlighted in blue:
andi r2, r5, 255
Both branches do not take the same time to reach their first post-dominator (and, r2, r4, r11): If the branch is taken, it takes 6 cycles, if not, it takes 12 cycles. So we can deduce that the time depends on the branch condition (r5).
This problem can be fixed by modifying the original C code. Instead of:
if((b & 1) == 1) p ^= a;
We put:
if((b & 1) == 1) {
p ^= a;
} else {
asm volatile( "nop" );
asm volatile( "nop" );
}
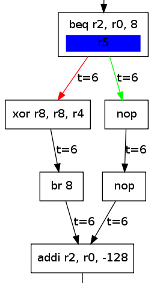
We causes the following graph to be generated (only the relevant branch is shown here):
As one can see, both branches now take the same time (18 cycles), and the execution time does not depend on r5 (b) anymore.
Note: This solution is actually suboptimal. The left side of the control flow graph could contain only the xor operation, and the right side could only contain a br operation, as follows:
bne r2, r0, 4 // If r2 != 0, jump to the xor br 4 // r2 == 0, jump over the xor to the addi xor r8, r8, r4 addi r2, r0, -128
But getting gcc to generate such code is tricky, and would require modifying directly the assembly code, which we did not want to do for the sake of simplicity.
Experimental setup
To be able to test experimentally if our system is able to detect time dependencies correctly, we programmed the following system on a FPGA4U:
- Nios II/e CPU (multi-cycle soft-core processor provided by Altera)
- On-chip SRAM for code and data (deterministic memory access time)
- Timer to measure execution time
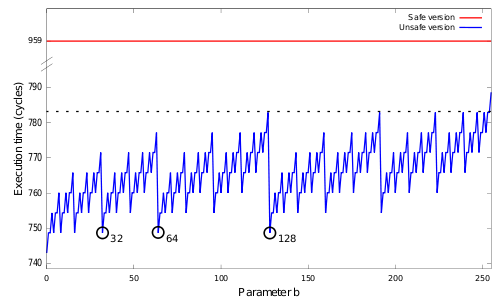
We then programmed some software containing the gmul and gmul_safe functions mentioned above, and measured the execution time depending on the parameter b.
On this graph, one can easily see that the execution time of the “unsafe” version (gmul) depends on the parameter b. More specifically, it depends on the number of 1 in the binary encoding of b. The relevant numbers have been encircled. Clearly, when b = 128 (0y10000000), the execution time will be small compared to b = 127 (0y1111111). Thus, if an attacker sees that the execution time is 782, it can obtain more information about the key. In this case, a subset of keys lying on the 782th cycle can be defined, shortening the number of tries (in case of bruteforce for instance): {127, 191, 223, 239, 247, 251, 253, 254}, ie the set of numbers whose binary representation contains “only one zero”.
However, the “safe” version's execution time does not depend on b, as indicated by our analysis tool, also, this execution time is more important than with the “unsafe” version, as nops had to be added, which seem to prevent gcc from doing relevant optimisations.
If the time dependency is solved in this example, an attacker could still perform a power analysis, based on the assumption that a NOP instruction will possibly consume less energy that a MUL instruction.
Conclusion & Going further
The tool works well with small functions. As soon as we are dealing with a whole program, the analysis might become slower.
Furthermore, only memory operations directly related to the stack pointer are handled. For a more complete analysis, it would be could to be able to handle other memory operations such as accessing global variables. Furthermore, indirect jumps cannot be handled by the tool, as they would require much deeper and complicated analysis.
Additionally, if a register is modified in the same way in 2 branches of an operation, we consider this register as dependent on the branch condition, which is actually wrong and may lead to false positives. We considered this as a minor problem, since the compilation process usually includes a common sub-expression elimination part which will move such operations before the branch instruction to reduce program size.
If we considered the time as a variable (just like registers), we could redefine any assembly instruction as a couple of register and time operation. For example, the instruction:
addi r2, r4, 4
would be redefined as:
r2 = r4 + 4; t = t + 6;
Then, we could symbolically execute both branches, and, when 2 branches merge, we could check not only if the time spent since the branch instruction is identical, but also if registers value depend on which branch is taken. This would in fact fix the potential problem seen above, while handling time dependencies in a more elegant way.
The tool currently provides good results with the very simple CPU we are using. Also, execution time of any given instruction can be determined statically (except shifting by a register value, but we decided not to handle this case). An improvement would be to use a more complex processor, i.e. with an architecture that you could find in more complex devices. This would however make the analysis much more complicated, as we should treat prediction, pipelining, and caching effects
References
- Mikael Buchholtza, Stephen Gilmoreb, Jane Hillstonb, Flemming Nielsona. Securing Statically-verified Communications ProtocolsAgainst Timing Attacks, ELSEVIER 2005.
- Travis Goodspeed's Blog. Blog entry on timing atacks.
- Andrew C. Myers, JFlow: practical mostly-static information flow control. Annual Symposium on Principles of Programming Languages 1999.
- Manuel Egele, Christopher Kruegel, Engin Kirda. Dynamic Spyware Analysis. Usenix 2007: particularly “3.2 Dynamic Taint Propagation”, which explains Data dependencies and Control dependencies (using post-dominators to know the scope of a particular branch instruction)
- Loukas Georgiadis, Renato F. Werneck, Robert E. Tarjan, Spyridon Triantafyllis and David I. August. Finding Dominators in Practice. Journal of Graph Algorithms and Applications vol. 10, no. 1, pp. 69-94 (2006): explains how to find dominators (post-dominators can be computed using the same algorithm, but with graph arcs inverted), 2.1 gives a very simple (and totally inefficient) algorithm to compute those.
- Wikipedia. Dominator (graph theory)