Comparing Fixpoints of Sequences
Lemma: Let 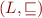 be a lattice and let
be a lattice and let  and for
and for  be sequences such that for each
be sequences such that for each  there
exists
there
exists 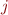 such that
such that  . Suppose that there exist
. Suppose that there exist  and
and 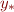 (e.g. if
(e.g. if  is a complete lattice) such that
is a complete lattice) such that
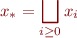
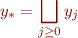
Then  .
.
Proof: Take any  . Then there is
. Then there is 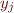 such
such
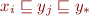
Thus, 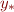 is an upper bound on the set
is an upper bound on the set 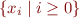 . Because
. Because  is the least upper bound,
is the least upper bound,  .
End of Proof.
.
End of Proof.