Problem 1
Galois connection is defined by two monotonic functions  and
and 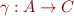 between partial orders
between partial orders  on
on  and
and  on
on  , such that
, such that

for all  and
and  (intuitively, the condition means that
(intuitively, the condition means that  is approximated by
is approximated by  ).
).
Part a) Show that the condition  is equivalent to the conjunction of these two conditions:
is equivalent to the conjunction of these two conditions:
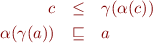
hold for all  and
and  .
.
Part b) Let  and
and  satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
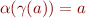 for all
for all 
 is a surjective function
is a surjective function is an injective function
is an injective function
Part c) State the condition for 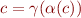 to hold for all
to hold for all  . When
. When  is the set of sets of concrete states and
is the set of sets of concrete states and  is a domain of static analysis, is it more reasonable to expect that
is a domain of static analysis, is it more reasonable to expect that 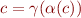 or
or 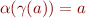 to be satisfied, and why?
to be satisfied, and why?
Problem 2
Suppose you are given a set of predicates 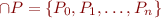 in a decidable theory of first-order logic (for example, quantifier-free formulas in the combination of uninterpreted function symbols with integer linear arithmetic) where
in a decidable theory of first-order logic (for example, quantifier-free formulas in the combination of uninterpreted function symbols with integer linear arithmetic) where 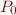 is the predicate 'false'.
is the predicate 'false'.
Part a) Consider Conjunctions of Predicates as abstract interpretation domain. Give example showing that it need not be the case that
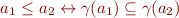
Part b) Describe how to construct from  a new, smaller, lattice
a new, smaller, lattice  , where the above equivalence holds. Is there an algorithm to compute
, where the above equivalence holds. Is there an algorithm to compute  and the partial order on
and the partial order on  using a decision procedure for the logic of predicates?
using a decision procedure for the logic of predicates?
Part c) Suppose that, for the same set of predicates, we use lattice  and lattice
and lattice  to compute the fixpoints
to compute the fixpoints 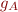 and
and 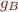 of the function
of the function  from Abstract Interpretation Recipe. What can you say about
from Abstract Interpretation Recipe. What can you say about
- the comparison of numbers of iterations needed to compute the fixpoint
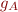 and
and 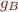 (is one always less than the other, can they be equal, does it depend on set
(is one always less than the other, can they be equal, does it depend on set 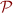 of predicates)
of predicates) - the precision of computed information, that is, comparison of sets
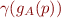 and
and 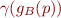 for an arbitrary program point
for an arbitrary program point  .
.