LARA

Abstract Interpretation with Conjunctions of Predicates

Parameters: a finite set of formulas 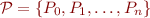${\cal P} = \{ P_0, P_1,\ldots,P_n\}$ in program variables. Suppose 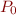$P_0$ is the predicate 'false'.

Let 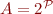$A = 2^{\cal P}$, so for $a \in A$ we have $a \subseteq {\cal P}$.

We design analysis using Abstract Interpretation Recipe.

Define a syntactic order on 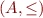$(A,\le)$

Finite lattice.

Defining $\gamma$.

Defining $\alpha$.

Is it the case that 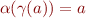$\alpha(\gamma(a))=a$?

Using a theorem prover to compute $sp^\#$.