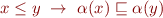Partial Orders
Partial ordering relation is a binary relation  that is reflexive, antisymmetric, and transitive, that is, the following properties hold for all
that is reflexive, antisymmetric, and transitive, that is, the following properties hold for all 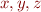 :
:
If  is a set and
is a set and  a binary relation on
a binary relation on  , we call the pair
, we call the pair 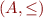 a partial order.
a partial order.
Given a partial ordering relation  , the corresponding strict ordering relation
, the corresponding strict ordering relation  is defined by
is defined by 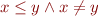 and can be viewed as a shorthand for this conjunction.
and can be viewed as a shorthand for this conjunction.
We can view partial order 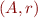 as a first-order interpretation
as a first-order interpretation 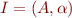 of language
of language 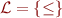 where
where 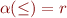 .
.
Example Partial Orders
Orders on integers, rationals, reals are all special cases of partial orders called linear orders.
Given a set  , let
, let  be any set of subsets of
be any set of subsets of  , that is
, that is  . Then
. Then 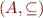 is a partial order.
is a partial order.
Example: Let 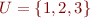 and let
and let 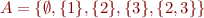 . Then
. Then 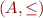 is a partial order. We can draw it as a Hasse diagram.
is a partial order. We can draw it as a Hasse diagram.
Hasse diagram
Hasse diagram presents the relation as a directed graph in a plane, such that
- the direction of edge is given by which nodes is drawn above
- transitive and reflexive edges are not represented (they can be derived)
Extreme Elements in Partial Orders
Given a partial order 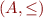 and a set
and a set  , we call an element
, we call an element 
- upper bound of
 if for all
if for all  we have
we have 
- lower bound of
 if for all
if for all  we have
we have 
- minimal element of
 if
if  and there is no element
and there is no element  such that
such that 
- maximal element of
 if
if  and there is no element
and there is no element  such that
such that 
- greatest element of
 if
if  and for all
and for all  we have
we have 
- least element of
 if
if  and for all
and for all  we have
we have 
- least upper bound (lub, supremum, join,
 ) of
) of  if
if  is the least element in the set of all upper bounds of
is the least element in the set of all upper bounds of 
- greatest lower bound (glb, infimum, meet,
 ) of
) of  if
if  is the greatest element in the set of all lower bounds of
is the greatest element in the set of all lower bounds of 
Taking  we obtain minimal, maximal, greatest, least elements for the entire partial order.
we obtain minimal, maximal, greatest, least elements for the entire partial order.
Duality minimal/maximal, least/greatest, supremum/infimum
Notes
- minimal element need not exist:
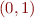 interval of rationals
interval of rationals - there may be multiple minimal elements:
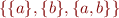
- if minimal element exists, it need not be least: above example
- there are no two distinct least elements for the same set
- least element is always glb and minimal
- if glb belongs to the set, then it is always least and minimal
- for relation
 on sets,
on sets, 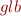 is intersection,
is intersection,  is union (not all families of sets are closed under
is union (not all families of sets are closed under  ,
,  )
)
Monotonic functions
Given two partial orders 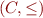 and
and 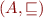 , we call a function
, we call a function  monotonic iff for all
monotonic iff for all 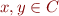 ,
,