Tarski's fixed point theorem
Let 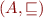 be a complete lattice and
be a complete lattice and 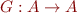 a monotonic function.
a monotonic function.
Definition:
 - the set of postfix points of
- the set of postfix points of  (e.g.
(e.g.  is a postfix point)
is a postfix point)
 - the set of prefix points of
- the set of prefix points of 
 - the set of fixed points of
- the set of fixed points of  . Note that
. Note that  .
.
Theorem: Let  . Then
. Then  is the least element of
is the least element of  (dually,
(dually,  is the largest element of
is the largest element of  ).
).
Proof.
In fact, the set of all fixpoints  is a lattice itself.
is a lattice itself.
Tarski's Fixed Point theorem shows that in a complete lattice with a monotonic function  on this lattice, there is at least one fixed point of
on this lattice, there is at least one fixed point of  , namely the least fixed point
, namely the least fixed point  .
.
Iterating Sequences and Omega Continuity
Tarski's theorem guarantees fixpoints in complete lattices, but the above proof does not say how to find them.
How difficult it is to find fixpoints depends on the structure of the lattice.
Let  be a monotonic function on a lattice. Let
be a monotonic function on a lattice. Let  and
and 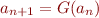 . We obtain a sequence
. We obtain a sequence  . Let
. Let 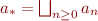 .
.
Lemma: The value  is a prefix point.
is a prefix point.
Observation:  need not be a fixpoint (example in exercises, e.g. on lattice [0,1] of real numbers).
need not be a fixpoint (example in exercises, e.g. on lattice [0,1] of real numbers).
Definition: A function  is
is  -continuous if for every chain
-continuous if for every chain  we have
we have
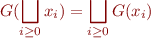
Lemma: For an  -continuous function
-continuous function  , the value
, the value  is the least fixpoint of
is the least fixpoint of  .
.
Proof:
By definition of  -continuous we have
-continuous we have 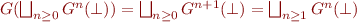 .
.
But 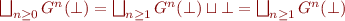 because
because  is the least element of the lattice.
is the least element of the lattice.
Thus 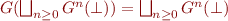 and
and  is a fixpoint.
is a fixpoint.
Now let's prove it is the least.
Let  be such that
be such that 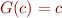 . We want
. We want 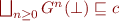 . This is equivalent to
. This is equivalent to  .
.
We can prove this by induction :  and if
and if 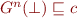 , then by monotonicity of
, then by monotonicity of  and by definition of
and by definition of  we have
we have 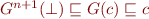 .
.
When the function is not  -continuous, then we obtain
-continuous, then we obtain  as above (we jump over a discontinuity) and then continue iterating. We then take the limit of such sequence, and the limit of limits etc., ultimately we obtain the fixpoint.
as above (we jump over a discontinuity) and then continue iterating. We then take the limit of such sequence, and the limit of limits etc., ultimately we obtain the fixpoint.
 range over elements of
range over elements of  .
.
 we get
we get 
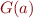 is a lower bound on
is a lower bound on 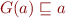


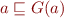
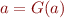 , so
, so 