More Efficient Handling of Conjunctions in DNF
Although we can replace equalities with two inequalities, this is typically inefficient way to handle them.
If the coefficient next to a variable is one, then we can just solve for this variable and use one-point rule.
What if the coefficient is not one? In that case we use techniques for solving linear Diophantine equations (=linear equations over integers).
Here is an example illustrating the key ideas.
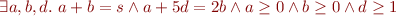
See more in e.g. in Hermite normal form.
Question: what if instead of 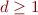 we had
we had 