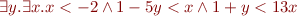Lab 03: Quantifier Elimination

Exercise 1

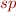If instead of good states we look at the complement set of error states, the $wp$ corresponds to doing $sp$ backwards.
In other words, for 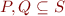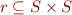$P,Q\subseteq S$ , $r \subseteq S \times S$ , the following holds:

$\begin{equation*} S \setminus wp(r,Q) = sp(S \setminus Q,r^{-1}) \end{equation*}$

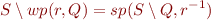
Prove this statement.

Quantifier Elimination

QE for Presburger Arithmetic
Here is also a PDF that does not have any folding/missing content issues.

More Efficient Handling of Conjunctions in DNF

More efficient handling of disjunctions and divisibility: see the Calculus of Computation textbook

Additional information:

Synthesis through Quantifier Elimination

Recall Hoare triple:

$\begin{equation*} \{ P \} r \{ Q \} \end{equation*}$

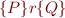
We have also seen how to do the following (at least for Presburger arithmetic):

given 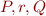$P, r, Q$ , check if the condition holds
given $P$ and $r$ , compute the strongest $Q$
given $r$ and $Q$ , compute the weakest $P$

How can we compute:

given $P$ and $Q$ compute the largest relation $r$ such that the triple holds (hint: it is easy!)

But how to do functional synthesis:

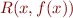given $r$ , find a (deterministic) function $f$ in our programming language such that $R(x,f(x))$ whenever $\exists y.. R(x,y)$ .

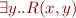Here is one approach:

Slides about Complete Functional Synthesis

Exercise 2

Eliminate quantifiers in the following formula in Presburger arithmetic.

$\begin{equation*} \exists y. \exists x. x < -2 \wedge 1 - 5y < x \wedge 1 + y < 13x \end{equation*}$