Extending Languages of Decidable Theories
Recall from Quantifier elimination definition that if 
has effective quantifier elimination and there is an algorithm for deciding validity of ground formulas, then the theory is decidable. Now we show a sort of converse.
Lemma: Consider a set of formulas . Then there exists an extended language 
and a set of formulas 
such that has effective quantifier elimination, and such that 
is exactly the set of those formulas in 
that contain only symbols from 
.
Proof:
How to define 
?
of all first-order variables. If 
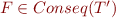is a term, formula, or a set of formulas, let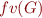 
denote the ordered list of its free variables.
denote the set of formulas in language 
. Define
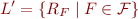
is a new relation symbol whose arity is equal to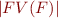 
. In other words, we introduce a relation symbol for each formula of the original language.
in language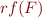 
, which is a formula in the original language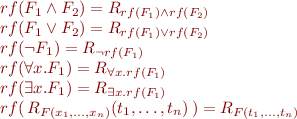 
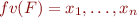is the sorted list of its free variables.
How to define ?
How to do quantifier elimination in ?
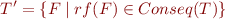
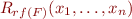where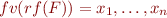 
. This quantifier elimination is easy and effective (and trivial).
End Proof.
Question: When is the question 
for from the proof decidable for ground formulas?
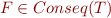is decidable.
Note: often we can have nicer representations instead of 
, but this depends on particular theory.