List of Some Theories Admitting QE
Presburger Arithmetic
As we have just seen in QE for Presburger Arithmetic.
Boolean Algebras with Presburger Arithmetic
Term Algebra
Formulas that are true in Herbrand interpretations of a language with no relation symbols (only equality).
A language containing arbitrary function symbols and constants. If  is set of ground terms over
is set of ground terms over  , we consider the class of interpretations
, we consider the class of interpretations 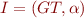 where
where

The question of whether terms are unifiable,
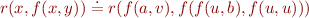
becomes the truth value of

in this theory. We can express more complex constraints.
- On the Theory of Structural Subtyping (see also citations in there)
Feature Trees
Related to term algebras.
Term Powers
Combines term algebras with products.
Knuth-Bendix Orders
Extends term algebras with ordering that is used in paramodulation provers.
Products of Structures admiting QE
Fefeman-Vaught theorem:
- reduce the truth value of quantified formulas over sequences of elements to truth value of formulas over elements
- the operations on sequences are defined point-wise
More information in references cited here:
Example: Consider logic that quantifies over pairs of integers and where addition is given by
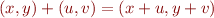

Formulas in such logic, where variables range over pairs, can be reduced to Presburger arithmetic.
Moreover, such reduction can be done even when variables range over infinite sequences of integers
Positive Integers with Multiplication
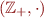 where
where  are positive integers and
are positive integers and  is multiplication.
is multiplication.
Consider prime factor representation of integers:
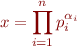
where 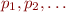 is sequence of prime numbers and
is sequence of prime numbers and  .
.
The structure is isomorphic to: 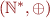 where
where 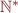 are finite sequences of exponents. Operation
are finite sequences of exponents. Operation  is vector addition.
is vector addition.
We can have only addition or only multiplication, but not both!
The Field of Complex and Real Numbers
Over complex numbers, we get decidability for both multiplication and addition - theory of polynomials.
- Upcoming excellent book by John Harrison
Mixed Linear and Integer Constraints
Linear arithmetic over rationals ( ,
,  , multiplication by rational constants) with operator, for
, multiplication by rational constants) with operator, for  ,
,
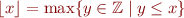
Observe that this also subsumes Presburger arithmetic.
References
- Wilfrid Hodges: Model Theory