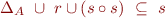Lab 02 - Relations
In this lab we'll practice some (more formal) proofs, hence show all steps in the exercises.
You may find the pages on First-order logic and
Sets and Relations helpful.
Exercise 1 - Relations, a warm up
Prove the following or give a counterexample.
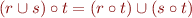
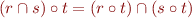


- If
 then
then  and
and  .
. - If
 then
then 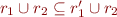 and
and 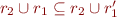 .
.
Note that the last two properties, if they hold, specify that relation composition and union are monotone.
Exercise 2 - Monotonicity
Let 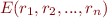 be a relation composed of relations
be a relation composed of relations  with an arbitrary combination of relation composition and union, that is the expressions
with an arbitrary combination of relation composition and union, that is the expressions  are trees with leaves being relations
are trees with leaves being relations  .
Show that this operation is monotone, that is show that for any
.
Show that this operation is monotone, that is show that for any 
 .
.
As an illustration, one possible expression could be 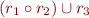 , then if
, then if  then
then  .
.
Exercise 3 - Relation of an entire program
Compute the relations for these programs. The final formulas cannot be expressed in Presburger arithmetic, for the sake of this exercise we'll allow any arithmetic you seem fit.
x = x * y
if (z > 5) {
y = y + x
x += 1
} else {
havoc(z)
y = y - x
}
while ( x < 100 ) {
y = y + 1
x = x * 2
}
Exercise 4 - Transitive closure
Suppose 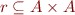 .
Show that the following 4 definitions of transitive closure are equivalent:
.
Show that the following 4 definitions of transitive closure are equivalent:

- the least relation
 (with respect to
(with respect to  ) that satisfies:
) that satisfies: 
- the least relation
 (with respect to
(with respect to  ) that satisfies:
) that satisfies: 
- the least relation
 (with respect to
(with respect to  ) that satisfies:
) that satisfies: