Lab 02 - Partial solution of Exercise 4
We will show that the first two statements are equivalent.
Let  and
and 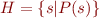 .
Note that the full relation
.
Note that the full relation  satisfies
satisfies  , hence the intersection is well-defined.
, hence the intersection is well-defined.
Then we claim that 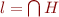 is the least relation
is the least relation  satisfying
satisfying  .
It is least, since
.
It is least, since 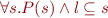 by the properties of intersection.
It remains to show that
by the properties of intersection.
It remains to show that  itself satisfies
itself satisfies  , i.e. that
, i.e. that 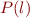 .
.
Now we claim 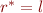 , i.e.
, i.e. 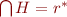 .
.
1)
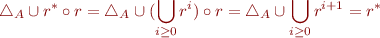
Hence, we have shown that 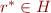 and thus
and thus 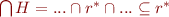 .
.
2)
From  , we have that
, we have that 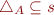 .
.
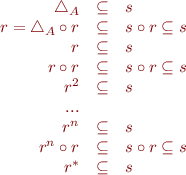
Hence, 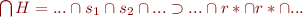 . Thus we have shown
. Thus we have shown 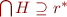 .
.
From 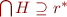 and
and 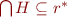 it follows that
it follows that 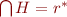 .
.