Lab 02, Solution of Exercise 2
We will show this by structural induction on the expression trees.
Suppose we have  for some fixed
for some fixed  .
Note that when writing
.
Note that when writing  ,
we mean the subset on relations represented by the expressions.
,
we mean the subset on relations represented by the expressions.
Base case
The expression  is just a leaf, i.e.
is just a leaf, i.e. 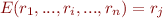 for some
for some 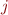 . Then either
. Then either 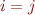 and
and
 follows directly from
follows directly from  .
Otherwise,
.
Otherwise,  , but in this case
, but in this case  , since
, since 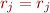 , so the result follows.
, so the result follows.
Inductive case
Now suppose monotonicity holds for two expressions  and
and  . Hence, denoting the relations represented by these expressions
by
. Hence, denoting the relations represented by these expressions
by 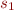 and
and  respectively,
respectively,  and
and  , where the primed version come from
replacing
, where the primed version come from
replacing  by
by 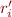 in
in  and
and  .
.
Let  . By
. By
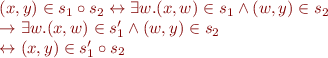
sequential composition preserves monotonicity and so  .
.
Now let  . Since
. Since
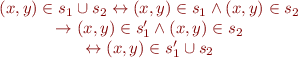
union preserves monotonicity and so  .
.