Collecting Semantics for Example Program
The general form of collecting semantics is:
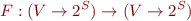
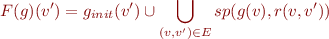
Here 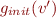 will be
will be  except at the entry into our control-flow graph.
except at the entry into our control-flow graph.
Example Program with One Variable
// v0 x := 0; // v1 while (x < 10) { // v2 x := x + 3; } // v3
Concrete Domain: Sets of States
Because there is only one variable:
- state is an element of
 (value of
(value of  )
) - sets of states are sets of integers,
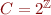 (concrete domain)
(concrete domain) - for each command
 , strongest postcondition function
, strongest postcondition function 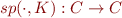
Strongest Postondition
Compute 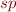 or example statements:
or example statements:
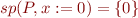
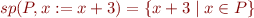
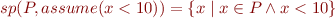
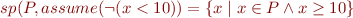
Sets of States at Each Program Point
Collecting semantics computes with sets of states at each program point
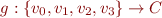
We sometimes write  as a shorthand for
as a shorthand for 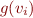 , for
, for 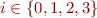 .
.
In the initial state the value of variable is arbitrary: 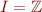
post Function for the Collecting Semantics
From here we can derive  that maps
that maps  to new value of
to new value of  :
:
![Equation \begin{equation*}
\begin{array}{l}
F(g_0,g_1,g_2,g_3) = \\
\begin{array}[t]{l}
(\mathbb{Z}, \\
sp(g_0, x:=0) \cup sp(g_2, x:=x+3),\\
sp(g_1, assume(x < 10)), \\
sp(g_1, assume(\lnot(x<10))))
\end{array}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img72fbfe992fe55bd85d8c7cb45f21a0c3.png)
The fixpoint condition 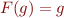 becomes a system of inequations
becomes a system of inequations
![Equation \begin{equation*}
\begin{array}[t]{l}
g_0 = \mathbb{Z} \\
g_1 = sp(g_0, x:=0) \cup sp(g_2, x:=x+3)\\
g_2 = sp(g_1, assume(x < 10)) \\
g_3 = sp(g_1, assume(\lnot(x<10))))
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgf68ae8019da653a6d906bff1c0b3e43b.png)
whereas the postfix point (see Tarski's fixpoint theorem) becomes
![Equation \begin{equation*}
\begin{array}[t]{l}
\mathbb{Z} \subseteq g_0 \\
sp(g_0, x:=0) \cup sp(g_2, x:=x+3) \subseteq g_1 \\
sp(g_1, assume(x < 10)) \subseteq g_2 \\
sp(g_1, assume(\lnot(x<10))) \subseteq g_3
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img987ce92c14d81680beeb5ea21f8861b9.png)
Computing Fixpoint
To find fixpoint, we compute the sequence 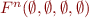 for
for  :
:
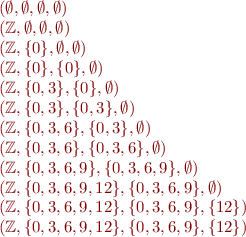
Thus, all subsequent values remain the same and 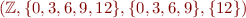 is the fixpoint of collecting semantics equations. In general we may need infinitely many iterations to converge.
is the fixpoint of collecting semantics equations. In general we may need infinitely many iterations to converge.
Question: Suppose that we have a program that terminates for every possible initial state. Can we always find a finite constant  such that
such that
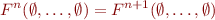
i.e. the sequence such as the one above is guaranteed to stabilize?
Example: Assume an arbitrary initial value and consider the loop. Compute a sequence of sets of states at the point after the increment statement in the loop, following the equations for collecting semantics.
if (y > 0) {
x = 0
while (x < y) {
x = x + 1
}
}
What always works from omega continuity:
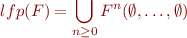
where  on a tuple above means taking union of each component separately, so
on a tuple above means taking union of each component separately, so 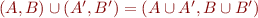 .
.