LARA

LR Parsing with Lookahead Items

Although SLR Parser Actions use lookahead, their finite state machine is computed without considering lookahead

LR(k) parser uses more general LR(k) items

We explain LR(1)

LR(1) item is (X::=p.q,a), written 

X ::= p.q    a

where

  • X::=p.q is a dotted production (LR(0) item)
  • 'a' is lookahead that must follow X

Closure and Goto for Sets of LR(1) Items

They generalize such functions for LR(0) parser in Automata for LR Parsing without Lookahead

closure(I) uses first(…) function to select correct lookahead

closure(I) is least set such that

  • I $\subseteq$ closure(I)
  • if (Y::=r) is a rule and 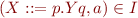$(X::=p.Yq, a)\in I$, and w $\in$ first(qa), then (Y::=.r, w) $\in$ closure(I)

goto is entirely analogous as before (using new closure):

\begin{equation*} goto(I,X) = closure(\{ (Y::=qX.r,a) \mid (Y::=q.Xr,a)\in I \}) \end{equation*}

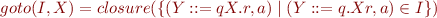
LALR(1) Items

The set of reachable LR(1) states can be large

LALR(1) uses a smaller set of states by merging some LR(1) states

Let nolook(I) denote removal of lookahead

\begin{equation*} nolook(I) = \{(X::=p.q) \mid (X::=p.q, a) \in I \} \end{equation*}

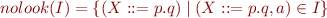
then if nolook(I)=nolook(J), we merge I and J (and replace them with $I \cup J$)

Note: this is better than SLR because

  • we first compute automaton using lookahead items
  • only then merge them

This is a popular approach

  • well-known 'yacc' parser generator