Variable Capture
We introduce informally concept of variable capture in Lambda Calculus
The expressions such as 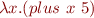 and
and 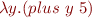 denote the same thing, namely a function that differ only by names of bound variables.
denote the same thing, namely a function that differ only by names of bound variables.
- we say one expression was obtained by another by
 -renaming
-renaming
Sometimes we need to do  -renaming before applying substitution in beta reduction to ensure meaningful result
-renaming before applying substitution in beta reduction to ensure meaningful result
Example: 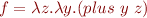 is an addition function. Therefore, we should have
is an addition function. Therefore, we should have
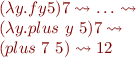
However, if we perform substitutions naively in certain order, we have the following:
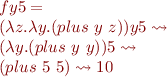
and therefore we have 
We obtained the wrong result!
This is because in step
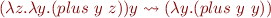
the variable  , which has scope outside of the expression became captured
, which has scope outside of the expression became captured
To avoid variable capture in this case, we first rename bound variable y to some fresh variable, e.g. x and then we have
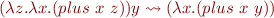
in which variable is not captured.