Lambda Calculus
Lambda calculus is a simple and powerful notation for defining functions. Among its uses are
- foundation of programming languages, especially functional languages such as Ocaml, Haskell, and Scala
- basis of higher order logic
In lambda calculus, functions have no side effects
- they are mathematical functions from arguments to results
- lambda calculus also supports higher-order functions
- this model is appropriate for studying type checking
- directly applicable to purely functional languages (like Haskell)
Anonymous Functions in Lambda Calculus
A function which takes its argument and increments it by 2 is given by lambda expression  . The
. The  operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition, writing
operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition, writing 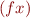 instead of
instead of 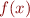 . Here are some example expressions and their values:
. Here are some example expressions and their values:
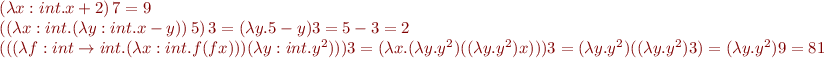
Concrete syntax for  :
:
Lambda Expressions
Abstract syntax of lambda expressions:
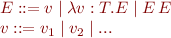
That is, an expression is 1) a variable, 2) a lambda expression defining a function, or 3) an application of one expression to another.
Certain predefined variables are called constants (e.g. 7, 42, 13, but also operations +, *).
Types are given by the following grammar:
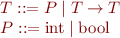
There can be additional primitive types  .
.
Currying
Instead of
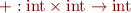
we have
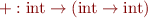
Therefore  is a function that increments its argument by
is a function that increments its argument by 
- expression
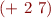 is just a shorthand for
is just a shorthand for 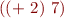
This is called currying in the honor of Haskell Curry
In general, instead of function
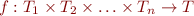
we can use function
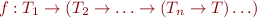
Beta Reduction
The main rule of lambda calculus is beta reduction, which formalizes function application:
![Equation \begin{equation*}
(\lambda x. e_1) e_2 = e_1[x:=e_2]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img642b7cbc7c3af1229e5b16771cef8844.png)
Here we assume capture-avoiding substitution
- we do renaming to avoid name clashes
Example:
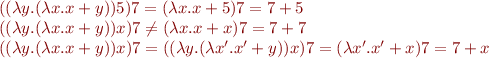
Rules for Constants
For each constant we have appropriate rule, for example we have
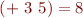
and so on, for each pair of integer constants. Similarly,
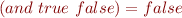
we can introduce conditional constant  , writing
, writing 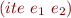 , with rules
, with rules
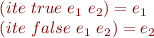
and so on.
If we get something like
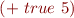
this is a run-time type error
- program would crash at run-time or produce bad result
- we introduce a type system to avoid this