Subtyping with Assignments and Generics
Named Variables
If a mutable variable named  has type
has type  , it means that it is guaranteed to be able to store values in
, it means that it is guaranteed to be able to store values in 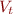
We cannot pretend that  can store values of supertype
can store values of supertype  because if we later read a value, we can unexpectedly get value that is not in
because if we later read a value, we can unexpectedly get value that is not in 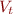
Assignment rule for named variables is therefore
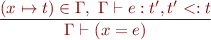
Reference Cells
Certain types denote memory regions that do not necessarily have static names
- mutable containers
- arrays
If  is a type, then
is a type, then 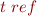 denotes values of references to cells that store values of type
denotes values of references to cells that store values of type 
Following language ML
- we write
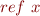 for a new cell storing value
for a new cell storing value 
- we write
 for reading content of reference
for reading content of reference 
- we write
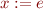 for storing values of
for storing values of  into cell referenced by
into cell referenced by 
In a Scala-like language, we would write ![Math $Ref[T]$](/w/lib/exe/fetch.php?media=wiki:latex:/img5c782cd7e3ace09842c769debfdc40bb.png) instead of
instead of 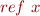 , and we would define
, and we would define
class Ref[T](var content : T)
We would write  instead of
instead of  , and write
, and write  instead of
instead of  .
.
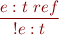
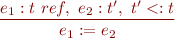
If  it
it
- does not imply that
 and it
and it - does not imply that

The only rule that applies is that if  then
then 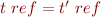
Examples
Note: To understand the following examples, note that (x : t ref ref) coresponds to (var x : t ref). In the example below, we therefore have mutable variables x and y, storing (pos ref) and (int ref). You can think of them as simply reference variables pointing to objects with a single mutable field, which we can extract with !x and assign to using :=. An assignment of the form x=y in Java here becomes x:=!y. The expression x:=y would not even type check and makes no sense because y has type of the form (t ref ref) but we expect type of form (t ref).
If we assume covariance, the program would type check and cause division by zero:
x : (pos ref) ref y : (int ref) ref z : int ref y := (!x); (!y) := 0; z = z / !(!x);
that is, in Scala:
var x : Ref[Pos] = Ref[Pos](1) var y : Ref[Int] = Ref[Int](-1) var z : Int y = x y.content = 0 z = z / x.content
If we assume contravariance, then replace y:=(!x) with x:=(!y) and it will type check and lead to same problem:
x : (pos ref) ref y : (int ref) ref z : int ref x := (!y); (!y) := 0; z = z / !(!x);
that is, in Scala:
var x : Ref[Pos] = Ref[Pos](1) var y : Ref[Int] = Ref[Int](-1) var z : Int x = y y.content = 0 z = z / x.content
Therefore, we have only the rule
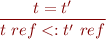
In Scala-like notation, Ref[S] <: Ref[T] only if S=T, it is not sufficient that S <: T, otherwise we would have examples like above that crash.