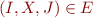Automata for LR Parsing without Lookahead
These automata are used to construct LR(0) and SLR parsers
We describe their states and transitions
LR(0) item is a dotted production 
 is grammar rule
is grammar rule 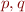 some strings of terminals and non-terminals
some strings of terminals and non-terminals
Note: this is similar to Earley Parser item
- but the initial position is thrown away
We use letters I,J to denote sets of LR(0) items
- approximates a set of paths in a possible syntax tree
- left side of tree corresponds to input seen so far
Again, if  was original start symbol, we
was original start symbol, we
- add (D'::=D EOF) to grammar
- make
 new start symbol
new start symbol
Closure and Goto Functions
These functions map sets of items to sets of items
Closure is similar to applying prediction in Earley Parser.
closure(I) is least set such that
- I
 closure(I)
closure(I) - if (Y::=r) is a rule and
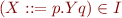 , then (Y::=.r)
, then (Y::=.r)  closure(I)
closure(I)
Goto corresponds to
- scan in Earley Parser when X is a terminal
- completion in Earley Parser when X is a non-terminal

Constructing Automaton
Initial state 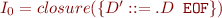
Edges are labeled by grammar terminals and non-terminals
- they are
 function of the Finite state machine
function of the Finite state machine
States and edges are the least sets (T,E) such that

- for each terminal and non-terminal
 and each
and each  , if
, if 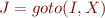 then
then
This automaton is deterministic
- empty set is dead state
- we do not represent dead state or its edges
Running automaton from initial state on stack results in state K
- the state K determines the action of LR parser
- if dead state, we have parse error