Earley Parser
What is Earley Parser
A parser for context-free grammars
- works for arbitrary, even ambiguous, grammars
- runs in O(n^3) in general
- unlike CYK Parsing Algorithm, it does not require Transforming to Chomsky Normal Form
- for unambiguous grammars it runs in O(n^2)
- for grammars handled by LR parsers, it runs in O(n)
Can be thought of as using dynamic programming, like CYK
- but driven by the input stream and start symbol (avoids unnecessary computation)
- like LR parsers uses notion of items
Items in Earley Parser
For right-hand sides of the form X::= UVW, a CYK Parsing Algorithm first uses Transforming to Chomsky Normal Form to introduce fresh non-terminals for partial right-hand sides, such as Z::=UV.
Earley parser instead uses grammar rules extended with exactly one 'dot' inserted, indicating the point reached by parser so far
X ::= UV.W
Call this a 'dotted production'.
We think of this as denoting non-terminal Z standing for UV.
CYK Parsing Algorithm uses a matrix d(i)(j) storing all non-terminals that can derive substring from i to j.
- instead of having e.g. d(i)(j) = {Z,P}, d(i')(j)={Q},
- use array d' storing non-terminals with their starting position: S(j)={(Z,i),(P,i),(Q,i')}
Earley parser stores at position j items (called states by Earley), which are pairs (X::=UV.W, i) of
- dotted right-hand side X::=UV.W
- starting position i
Note: for X::=UVW there are 4 dotted productions:
X::=.UVW X::=U.VW X::=UV.W X::=UVW.
Earley Parsing Idea
Input string: w(0) … w(N-1) EOF
Parser examines input left to right, computes S(i) for i from 0 to N-1
If D is start symbol in the original grammar, we add extra production
D'::=D EOF
and make D' start state, so parser can detect end of input.
Let  denote sequences of terminals and non-terminals of grammar.
denote sequences of terminals and non-terminals of grammar.
Goal: S(j) should contain all items that could appear in parsing of strings beginning with w(0),…,w(j-1)
More precisely: S(j) contains those items 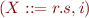 for
for  such that for some
such that for some 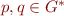

 is a grammar rule,
is a grammar rule, 
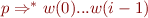
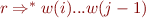
We sketch these conditions as follows:
w(0) ... w(i-1) w(i) ... w(j-1) w(j) ... w(N-1)
| | ^
| p | r | s? | |
| parser position
| X? | q? |
For 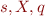 the parser did not check yet whether they agree with the input string.
the parser did not check yet whether they agree with the input string.
Steps of Early Parsing Algorithm
Initially, let S(0) = {(D'::=.D EOF,0)}
When scanning input at position j, parser does the following operations (p,q,r are sequences of terminals and non-terminals):
Prediction
If 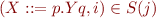 and
and  is a grammar rule, then
is a grammar rule, then
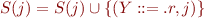
Scanning
If 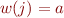 and
and 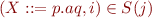 then (we can skip a):
then (we can skip a):
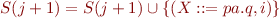
Completion
If 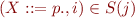 and
and 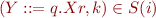 then
then
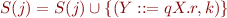
sketch of completion:
w(0) ... w(k) ... w(i) ... w(j)
| q | p |
Y::=q.Xr X::=p.
Y::=qX.r
Remarks on Complexity
We measure parsing time as a function of input length N, for a fixed grammar.
- fixed number of dotted rules
In S(j) there can be at most j copies of each dotted rule (for all possible start positions)
- prediction and scanning take O(N)
- completion can take O(N^2) (but size of result still O(N))
Summing up work over all S(j), we get O(N^3)
For ambiguous grammar, completion is proportional to its result, so it is O(N)
- overall parsing time is O(N^2)
- becomes O(N) if |S(j)| is independent of N (bounded-state grammars)
- if number of previous points in input to examine is bounded by constant