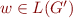Transforming a Grammar to Chomsky Form
We show how to make a grammar:
- without unproductive symbols
- without unreachable symbols
 -free (no non-start nullable symbols)
-free (no non-start nullable symbols)- without single productions X::=Y (X,Y non-terminals)
- without productions of arity more than two
- with terminals occurring alone on right-hand side
Elimination of Non-Productive Non-Terminals
Non-terminal is non-productive if it cannot generate any string of terminals
- if X::=w and w has only terminals, then X is productive
- if X:=p and p has only productive symbols, then X is productive
Start from empty set, apply these rules to compute productive symbols
- remaining symbols are non-productive
- delete them and all rules that contain them
Elimination of Unreachable Non-Terminals
Non-terminal is unreachable if no derivation from start symbol contains it
- S is reachable
- if X is reachable and X::=p, then every symbol in p is reachable
Start from empty set, apply these rules to compute productive symbols
- remaining symbols are non-productive
- delete them and all rules that contain them
Making Non-Terminals Non-Nullable
A grammar where is  -free if
-free if
- no-non terminal is nullable, or
- only S is nullable and S does not appear on right-hand side
First, compute nullable (see Lecture 03)
Then, for each production

create all productions of form

where
 is
is 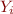 (as before), or,
(as before), or, 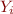 is nullable and
is nullable and  is empty string (so it disappears)
is empty string (so it disappears)
Remove all right-hand sides that are “”
If S is nullable, introduce new initial symbol S' and add
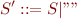
Eliminating Single Productions
Construct a directed graph of non-terminals between X,Y such that  is production
is production
Compute  as the transitive closure of this graph
as the transitive closure of this graph
If X  Y and Y ::= p is a rule, then add rule
Y and Y ::= p is a rule, then add rule
X ::= p
Then remove single productions.
Eliminating Non-Binary Productions
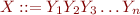
becomes
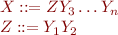
Making Terminals Alone on Right-Hand Side
Just introduce a fresh non-terminal 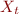 for terminal t
for terminal t
Use 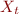 on RHS instead of t
on RHS instead of t
Add rule 
Summary of Parsing General Context-Free Grammars
To check if 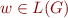 :
:
- Convert
 to equivalent Chomsky normal form
to equivalent Chomsky normal form 
- Use CYK Parsing Algorithm to check if