CYK Parsing Algorithm for General Context-Free Grammars

Given a context-free grammar $G$ , how to check if $w \in L(G)$ ?

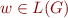recursive descent gives efficient answer when $G$ is LL(1)
we now see how to do it for arbitrary context-free grammar $G$

Conventions:

S will always denote the start symbol of the grammar
rules of grammar are always of the form $X ::= p$ where $p$ is a string of terminals and non-terminals

Chomsky Normal Form

A grammar is in Chomsky normal form if it has only these kinds of productions:

X ::= Y Z
X ::= t
S ::= ""

where

X,Y,Z denote non-terminals
t denotes terminals
S is the start non-terminal
if S::=“” appears, then S does not appear on right-hand side of another rule

Observe:

the empty string can only occur for the start non-terminal
terminals occur only by themselves on right-hand side
in parse tree, each non-terminal leads either to terminal or to two other non-terminals

Parsing a Chomsky Normal Form Grammar

Example Grammar

S ::= L R | S S | L X
X ::= S R
L ::= "{"
R ::= "}"

Consider an input string

{ { } { } { } }

For each terminal t in input, for which non-terminal X is it the case that X $\Rightarrow^* t$ ?

{ { } { } { } }   length of substring
L L R L R L R R      1
   S   S   S         2
            X        3
     S   S           4
          X          5
       S             6
         X           7
       S             8

For each string w of length 2 in input, for which non-terminal X is it the case that X $\Rightarrow^* w$ ?

Dynamic programming algorithm: for each substring, determine which non-terminals can generate it.

Let $w$ be input word

Let d(i)(j) denote non-terminals deriving substring 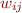$w_{ij}$ of $w$ from i to j.

$\begin{equation*} d(i)(j) = \{ X | (X::=Y Z) \in G,\ Y \in w_{ik},\ Z \in w_{k+1,j} \} \end{equation*}$

CYK algorithm:

  INPUT: word w, grammar G in Chomsky normal form
  OUTPUT: true iff (w in L(G))
  N = |w|
  var d : Array[N][N] 
  forall i != j : d(i)(j) = {}
  d(i)(i) = {X | G contains X->w(i)}

  for k = 2 to N // substring length
    for i = 0 to N-k // initial position
      for j = 1 to k-1 // length of first half
        for each (X::=Y Z) in G
          if Y in d(i)(i+j-1) and Z in d(i+j)(i+k-1)
            d(i)(j) = d(i)(j) union {X}
  return (S in d(0,N-1))

Example of Parsing

Consider this fragment of a grammar of language with references and procedure calls

statement ::= assign | call
assign ::= expr "=" expr
call ::= expr "." ID "(" expr ")"
expr ::= ID | expr "." expr

Is this grammar LL(1)?

What is its Chomsky Normal Form?

Additional information: