Prefix, Infix, and Postfix Notation

Let

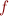$f$ be a binary operation and
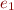$e_1$ , $e_2$ two expressions

We can write 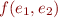$f(e_1,e_2)$ in

prefix notation	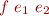$f\ e_1\ e_2$
infix notation	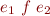$e_1\ f\ e_2$
postfix notation	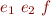$e_1\ e_2\ f$

Infix is the worst notation: it requires parantheses and parenthese, the other two do not!

prefix	+ x y	+ * x y z	+ x * y z	* x + y z
infix	x + y	x * y + z	x + y * z	x * (y + z)
postfix	x y +	x y * z +	x y z * +	x y z + *

---------
  +
 x y
---------
    +
  *   z
 x y
---------
   +
 x   *
    y z
---------
   *
 x   +
    y z
---------
      +
    +   u
  +   z
 x y
---------

prefix	+ + + x y z u	+ x + y + z u
infix	( ( x + y ) + z ) + u	x + (y + (z + u ))
postfix	x y + z + u +	x y z u + + +

---------
      +
    +   u
  +   z
 x y
---------
   +
 x   +
   y   +
      z u
---------

Other names:

prefix = Polish notation (attributed to Jan Lukasiewicz from Poland)
postfix = Reverse Polish notation (RPN)

Is the sequence of characters in postfix opposite to one in prefix?

Postfix will be of particular interest of us today