Proving Safety Properties using Types
We next discuss general techniques for proving absence of errors in programs
This also tells us how to prove that our type systems are meaningul (sound)
Safety Properties of Programs
Given a one-step reduction relation  , as in Operational Semantics of Lambda with Letrec, a finite execution is a sequence of states
, as in Operational Semantics of Lambda with Letrec, a finite execution is a sequence of states

where 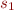 is one of the possible initial states of the program.
is one of the possible initial states of the program.
(We have seen an example of finite execution trace of lambda calculus with letrec.)
A safety property of a program is a property of finite executions of this program
In addition to safety, there are other kinds of properties, in particular liveness
- require reasoning about infinite executions
- example: the program always reaches a given program point
- explained in the EPFL course Model Checking taught by Prof. Thomas Henzinger
- in this compilers course we talk only about safety
Important kind of safety properties: program does not crash with a run-time error
We represent run-time errors using a predicate error(s) which is true iff s is a run-time error
- we do not wish to reach state s such that error(s)
A finite execution trace  is error-free iff
is error-free iff  for all
for all 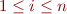
- this definition shows that “program cannot reach a run-time error” is a safety property
Examples of Run-Time Errors
Depending on the programming language, run-time errors can include
- null dereference in Java
- array bounds error in Java
- failed type cast in Java
- division by zero in Java
- attempt to multiply integer with a string
- attempt to invoke a non-existing method on an object in Smalltalk
Example Error in Python Program
Example program in the Python (programming language)
i = 40000000 while i > 0: i = i - 1 width = 30 height = 20 important = "learning" area = width * height fishy = important / height
Call this program 'test.py'
If you run it, you will first have to wait for a bit, and then you will get a result like this:
If you ask me:
- this is not very good, so if you invent a new python, add at least basic type checks
- some languages, like C, are even worse, because error may not be visible even at run-time
- whenever you read about vulnerability caused by buffer overflow, remember this is to large extend because C makes it impossible to detect errors even at run-time
If you did not play with python before, for your amusement evaluate in the python interpreter the expression
100*"I will not design bad languages. "
Example Error in Untyped Lambda Calculus
(% x. (ite x 7 8)) (+ (+ 5 3) 2) -> (% x. (ite x 7 8)) (+ 8 2) -> (% x. (ite x 7 8)) 10 -> ite 10 7 8
The last state is an error state, because the argument of 'ite' is not a boolean but a number
Proving Safety by Induction
Usually we use mathematical induction to prove safety (including absence of run-time errors)
- show a property for all traces of length zero
- show that if property holds for all traces of length
 , it holds for traces of length
, it holds for traces of length 
Problem: if 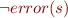 , it does not mean that there won't be error in
, it does not mean that there won't be error in 
- example: no error by step
 , but then program calls a method that will cause a run-time error in step
, but then program calls a method that will cause a run-time error in step 
- see above examples
As in many other examples, we typically need to strengthen the induction hypothesis
Example: straight-line program that uses int and boolean types
x = 3; y = bool; z = 70; --> z = z / x; x = x + 1; z = z / x;
Just because there was no error so far, it does not mean that later there will not be e.g. 'x = z / x' when x=0
We need a stronger induction hypothesis. For example, perhaps we can prove that all values of variables used after '/' are positive
We call a stronger induction hypothesis inductive invariant and denote it  . It is property for which inductive proof works:
. It is property for which inductive proof works:
- for each initial state
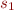 , we have
, we have 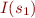
- if
 and
and 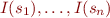 , then
, then 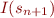
To prove absence of errors, we find an inductive invariant  that ensures absence of errors: for all configurations
that ensures absence of errors: for all configurations  ,
, 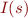 implies
implies
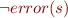 .
.
All states  in execution sequence satisfy
in execution sequence satisfy 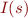 , so they satisfy
, so they satisfy 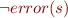
Ensuring Safety Using Types
One of the goals of static type systems is to ensure absence of crashes due to certain run-time type errors
We say that type system is sound if 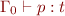 for program
for program  implies that execution of
implies that execution of  causes no run-time type errors of certain kind
causes no run-time type errors of certain kind
- example of errors prevented: adding int and bool values, calling non-existing method in Java
- some errors may remain: division by zero, null dereference
Because absence of errors is a safety property, we can prove it using an inductive invariant
Soundness theorem for a type system shows that if program type checks, then there is a property  or program configurations such that
or program configurations such that
 is an inductive invariant
is an inductive invariant implies that there are no run-time errors
implies that there are no run-time errors
If program configuration  is a program itself, then
is a program itself, then 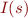 usually says that
usually says that  type checks
type checks
- if there is state, then it must talk about type checking in a given program state
- we can typically represent states as certain 'map' expressions
Summary of Type Soundness Proofs
To prove type soundness, we need to do the following:
- define program configurations and operational semantics

- show how to define property
 for a given program that type checks
for a given program that type checks - show that every such
 is an inductive invariant
is an inductive invariant - show that if
 holds, then certain run-time errors will not happen
holds, then certain run-time errors will not happen
We next see an example