Operational Semantics of Lambda Calculus with Letrec
We describe evaluation rules for our lambda calculus with letrec
We need such description to make rigorous proofs about compilers, including type systems
This is a mathematical description of an interpreter for this language
It is also analogous to relations that transform configurations in
- finite state machines
- push-down machines
Configuration in this case is simply an expression of lambda calculus with letrec
- for programming languages with state, configuration would also need to include (global and local) state, and stack
We define one-step relation on configurations, here denoted 
We write  to denote
to denote 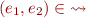
- meaning: one step of evaluating
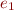 leads to
leads to 
Evaluation Rules for Operational Semantics
Evaluate Primitive Operation
Example 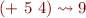
Depends on the set of primitive operators in the language
Beta Reduce
![Math $(\lambda x:T.e_1)e_2 \leadsto e_1[x:=e_2]$](/w/lib/exe/fetch.php?media=wiki:latex:/img43d826a48033d0e3655dff59c36c8561.png)
Letrec Base
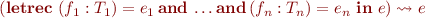
if  does not contain any of the variables
does not contain any of the variables 
Letrec Unfold
![Equation \begin{equation*}\begin{array}{l}
(\textbf{letrec}\ {(f_1:T_1)} = e_1\, \textbf{and}\, \ldots \textbf{and}\, {(f_n:T_n)} = e_n\ \textbf{in}\ e) \leadsto \\
(\textbf{letrec}\ {(f_1:T_1)} = e_1[f_1:=e_1,\ldots,f_n:=e_n]\, \textbf{and}\, \ldots \textbf{and}\,
{(f_n:T_n)} = e_n[f_1:=e_1,\ldots,f_n:=e_n]\,\ \textbf{in}\ e[f_1:=e_1,\ldots,f_n:=e_n])
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img55cbb62a7ce7bd4e17d23d1057d4b616.png)
Context Rule
![Equation \begin{equation*}
\frac{e \leadsto e'}
{C[e] \leadsto C[e']
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img4b2f5876b567697535b8306d30c44a16.png)
Here ![Math $C[e]$](/w/lib/exe/fetch.php?media=wiki:latex:/img14ed6fb2ef5d21d2a9c923e938e05a67.png) denotes expression containing one occurrence of
denotes expression containing one occurrence of  and
and ![Math $C[e']$](/w/lib/exe/fetch.php?media=wiki:latex:/img10d9bcae448de79fe786fde0335e92bd.png) results from
results from ![Math $C[e]$](/w/lib/exe/fetch.php?media=wiki:latex:/img14ed6fb2ef5d21d2a9c923e938e05a67.png) by replacing this ocurrence of
by replacing this ocurrence of  by
by 
Note: sometimes we pick a particular evaluation strategy
- eager: evaluate arguments of function application before unfolding function
- outermost: pick outermost expressions to evaluate
Example
Example of (outermost) evaluation:
letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (twice 1) -unfold-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in ((% x.(ite (<= x 0) 0 (+ 2 (twice (- x 1))))) 1) -beta-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (ite (<= 1 0) 0 (+ 2 (twice (- 1 1)))) -primitive(<=)--> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (ite false 0 (+ 2 (twice (- 1 1)))) -primitive(ite)--> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 (twice (- 1 1))) -primitive(-)--> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 (twice 0)) -unfold--> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 ((% x.(ite (<= x 0) 0 (+ 2 (twice (- x 1))))) 0)) -beta-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 (ite (<= 0 0) 0 (+ 2 (twice (- 0 1))))) -primitive(<=)-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 (ite true 0 (+ 2 (twice (- 0 1))))) -primitive(ite)-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in (+ 2 0) -primitive(+)-> letrec (twice:int->int) = % x.(ite (<= x 0) 0 (+ 2 (twice (- x 1)))) in 2 -base-> 2