Finite state machine
A finite state machine is a way of defining a language (see Strings and languages). We give a string to the machine, which examines the string one character by one, and at the end decides whether the string is the language or not.
A non-deterministic finite state machine (also called 'finite automaton') is a five-tuple  where
where
 is a finite alphabet
is a finite alphabet is a finite set of states
is a finite set of states is a transition relation
is a transition relation is the initial state of the automaton
is the initial state of the automaton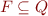 is the set of final states
is the set of final states
We graphically represent finite state machines using a graph.
- the nodes of the graph are the states
 , represented using circles
, represented using circles - the graph has an edge from
 to
to  labelled by
labelled by  if and only
if and only 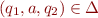
- we draw a double circle around each state
 if and only if
if and only if 
- we put a symbol
 in front of the initial state
in front of the initial state 
Example finite state machine:
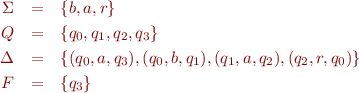
We formalize the operation of a finite state machine as follows.
If  and
and 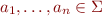 , an execution of a finite state machine
, an execution of a finite state machine 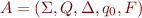 on
on  is a sequence
is a sequence
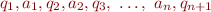
where 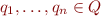 , such that
, such that 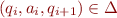 for all
for all 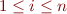 .
.
If 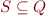 , we define
, we define 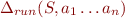 as the set of all states in which the automaton could be while processing the word
as the set of all states in which the automaton could be while processing the word  .
Formally, we define
.
Formally, we define 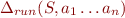 as the set of all states
as the set of all states  such that there exists an execution with given
such that there exists an execution with given  , with
, with  , and witn some
, and witn some 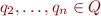 .
.
An accepting execution is an execution where  and
and 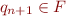 . We say that
. We say that  accepts the string
accepts the string  iff there exists an accepting execution of
iff there exists an accepting execution of  on
on  . We define the language of the automaton, denoted
. We define the language of the automaton, denoted 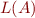 , as the set of all strings that
, as the set of all strings that  accepts.
accepts.
We then have
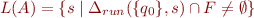
Example: the example automaton above accepts the language 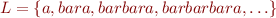 , which we can denote by
, which we can denote by  .
.
What is the automaton accepting strings of the form  where
where 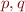 are arbitrary strings?
are arbitrary strings?
A state machine is called deterministic iff for every pair  there exists exactly one
there exists exactly one  such that
such that 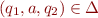 .
.
References