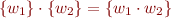Strings and languages
We next formalize mathematically the notion of a string and a set of strings.
Alphabet is a finite set of elements. (It represents characters of a string.) Let's denote it  .
.
A string is a potentially empty, finite sequence of alphabet elements. Often strings are called “words” in automata theory terminology. We use  to denote an empty string. We denote the set of all strings by
to denote an empty string. We denote the set of all strings by  . We can represent strings of length
. We can represent strings of length  by
by  -tuples, so we can define
-tuples, so we can define
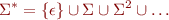
We use centered dot for string concatenation, as in  , and we sometimes omit it, as in
, and we sometimes omit it, as in 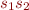 (programming language Objective Caml uses ^ to denote string concatenation; other languages often use + as an overloaded operator).
(programming language Objective Caml uses ^ to denote string concatenation; other languages often use + as an overloaded operator).
The concatentation is an operation  . It is associative, and
. It is associative, and  is left and right neutral element:
is left and right neutral element:
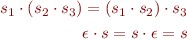
Therefore, 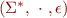 is a monoid.
is a monoid.
If  is a word, we define
is a word, we define 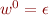 and
and 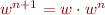 .
.
A language is any set of strings, that is, a set  .
.
Languages are sets, so operations 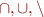 all apply to them.
all apply to them.
We define concatenation and iteration of languages by
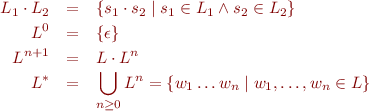
Simple Consequences
Observe that
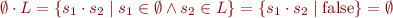
Similarly, 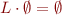 .
.
Also directly from definition follows: