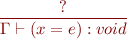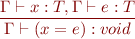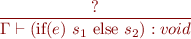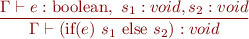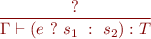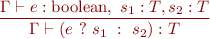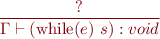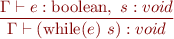Type Checking Rules for a Simple Language
Abstract Syntax of a Simple Language
This language is similar to one in Semantic Analysis as Simplified Interpretation, but for simplicity assumes programs have only one class (called World) and all members to are assumed to be static.
program ::= "class" "World" "{" varDecl* method* "}" method ::= varDecl "(" varDecl* ")" "{" stmt* "return" expr "}" varDecl ::= type ID type ::= "int" | "boolean" | "void" stmt ::= expr | if | while | block if ::= "if" expr stmt "else" stmt while ::= "while""("expr")" stmt block ::= "{" (stmt|varDecl)* "}" expr ::= ID | expr "+" expr | expr "<=" expr | assign | call | condExpr assign ::= ID "=" expr condExpr ::= expr "?" expr ":" expr call ::= ID "(" expr* ")"
Note: this is abstract, not concrete syntax
- some commas and semicolons are removed
- keywords and parantheses are kept to make rules clearer
- in the text below we do not use e.g. quotes around keywords
Remark on language:
- method call is an expression (resulting type is return type of method)
- assignment is an expression (resulting type is void, this will not work: x=y=z)
Notation for Type Rules
We write 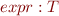 to indicate that
to indicate that
 is well-typed inside and has resulting type
is well-typed inside and has resulting type 
Examples:
Type rule for addition:
e1 : Int, e2 : Int
------------------
e1+e2 : Int
For <=:
e1 : int, e2 : int
------------------
e1<=e2 : boolean
Type derivation for
3 + 5 <= 9
is the following
3 : Int, 5 : Int
---------------- , 9 : Int
3 + 5 : Int
---------------------------
(3 + 5 <= 9) : boolean
Type Rule for Function Application
We have
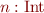




- for user-defined functions, rules are given by their declaration
The general rule for operation  is:
is:
- if
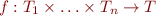 ,
, - and
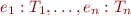 ,
, - then
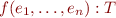
We write this as the following application typing rule:
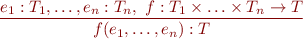
What does it correspond to in Semantic Analysis as Simplified Interpretation?
- checks in parameter passing, see insertArgs function
Type Rules with Environment
To know types of variables, type rules must refer to the environment.
Notation

means that in environment  , expression
, expression  is type correct and has type
is type correct and has type 
 is a partial function from names (of variables, operators, and methods) to types
is a partial function from names (of variables, operators, and methods) to types
Shorthand 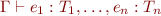 means
means  for
for 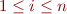
Variable rule with environment:
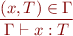
Function application rule with environment:
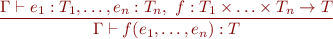
Type Rule for Entire Program
Given a program
class World {
Tg_1 xg_1;
...
Tg_n xg_n;
method1
...
methodM
}
The program is type correct if each method is type correct:
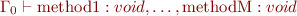
where the initial environment 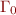 contains:
contains:
- types of predefined operators like
 ,
,  ,
,  and constants
and constants 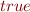 ,
, 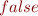 ,
,  ,
, 
- types of global variables,
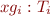 for each global variable declaration
for each global variable declaration 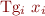
- types of declared methods: for each method definition
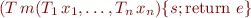
the environment 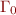 contains binding
contains binding

Type Rule for Method Bodies
Note that environment  already contains the expected type that the method is supposed to have.
already contains the expected type that the method is supposed to have.
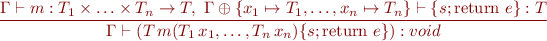
Here
 denotes overriding one map with another, as seen in Maps in Math
denotes overriding one map with another, as seen in Maps in Math- we give a dummy 'void' type to indicate that method is well-defined
- the assumption of type rule checks that the return type is correct
- later we present more elegant approach using lambda calculus
Type Rule for Method Calls
Method calls are just function applications:
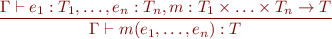
Type Rule for Assignment
Type Rule for If Statement
Type Rule for Conditional Expression
Type Rule for While Statement
Type Rules for Block Statement
Note that variable declarations are allowed in blocks
- we type statements one by one
- declarations introduce new bindings into the environment
We apply these rules (with those listed first having higher priority):
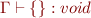

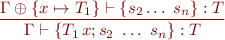
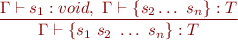
Using Rules in an Example
class World { boolean z; int u; int f(boolean y) { z = y; if (u > 0) { int z; z = f(u) + 3; return z+z; } else { return 0; } } }
Remarks
Seen notion of type rules through an example of a simple language
Advantages of rules versus semantic analyzer implementation:
- more concise
- precise meaning, make correctness proofs simpler
- more declarative
- we could execute them from top to bottom, but there are other interpretations