Using Finite State Machines to Build Lexers
Suppose we have token classes 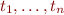 and each
and each  is given by regular expression
is given by regular expression  .
.
Consider building an automaton for 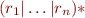
- a step towards solution
Example: Construct (directly) a finite state machine for these classes of tokens:
<, >, =, <=, =>, >=, ==, <=>
Verify whether it is minimal. Run it on the sequence
<==><==<=>
What can this automaton tell us about input character stream?
What we need is to compute the sequence of tokens
Modify state machine
- for each accepting state specify the token recognized (but do not stop)
- use token class priority if multiple options
- for longest match rule: remember last token and input position for last accepted state
- when no accepting state can be reached:
- revert position to last accepted state
- return last accepted token
Example: How to modify previous example to store the information needed?