Homework 06 - Due April 9
Problem 1
(Recall Definition of Resolution for FOL.)
Let 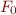 denote formula
denote formula
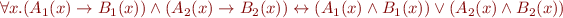
For each of the following formulas, if the formula is valid, use resolution to prove it; if it is invalid, construct at least one Herbrand model for its negation.
a): Formula 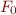
b): Formula
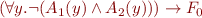
c): Formula
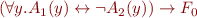
d): Formula
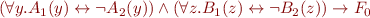
e): Formula:
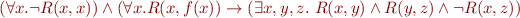
Problem 2
(Recall Sets and Relations.)
We say that a binary relation is a partial order iff it is reflexive, antisymmetric, and transitive. Let  be a non-empty set and
be a non-empty set and 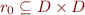 a binary relation on
a binary relation on  . Let
. Let 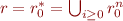 be the reflexive transitive closure of
be the reflexive transitive closure of 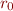 .
.
a) Give an example 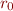 for which
for which  is not necessarily a partial order.
is not necessarily a partial order.
b) Define 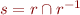 . Show that
. Show that  is a congruence with respect to
is a congruence with respect to  , that is:
, that is:  is reflexive, symmetric, and transitive and for all
is reflexive, symmetric, and transitive and for all 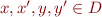 ,
,
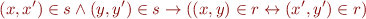
c) For each  let
let ![Math $[x] = \{ y \mid (x,y) \in s \}$](/w/lib/exe/fetch.php?media=wiki:latex:/img34cd05187f1375fc81be3dc1e49974ba.png) . Let
. Let ![Math $[D] = \{ [x] \mid x \in D\}$](/w/lib/exe/fetch.php?media=wiki:latex:/img325e4358d0a0dfbafcfc7daff36523f9.png) . Define a new relation,
. Define a new relation, ![Math $[r] \subseteq [D] \times [D]$](/w/lib/exe/fetch.php?media=wiki:latex:/imge46b953c575b6eadd3061e15a9f3cb97.png) , by
, by
![Equation \begin{equation*}
[r] = \{ ([x],[y]) \mid (x,y) \in r \}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgea264bca90bd6780ab26526ddd807847.png)
Show that ![Math $[r]$](/w/lib/exe/fetch.php?media=wiki:latex:/img8805783f428d9eceffcca44a82729afd.png) is a partial order on
is a partial order on ![Math $[D]$](/w/lib/exe/fetch.php?media=wiki:latex:/img550d21162531b5d992a255c2981c0e79.png) .
.
Optional: Explain this constructions using terminology of graphs and strongly connected components.
Problem 3
(Recall Substitutions for First-Order Logic, Unification.)
Let  be an infinite set of variables. Let
be an infinite set of variables. Let  be some first-order language. We will consider terms that contain variables from
be some first-order language. We will consider terms that contain variables from  and function symbols from
and function symbols from  .
.
Following Problem 2 above, let 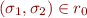 iff there exists substitution
iff there exists substitution  such that
such that 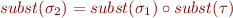 where
where  is the standard relation composition.
is the standard relation composition.
a) Compute 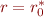 . What is its relationship to
. What is its relationship to 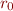 ?
?
b) Compute 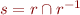 . Show that relation
. Show that relation  holds iff
holds iff 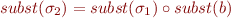 where
where  is a relation which is bijection on the set
is a relation which is bijection on the set  .
.
Optional: c) Let  be a fixed set of syntactic equations. Let
be a fixed set of syntactic equations. Let  be the set of unifiers for
be the set of unifiers for  and
and ![Math $[U] = \{ [\sigma] \mid \sigma \in U \}$](/w/lib/exe/fetch.php?media=wiki:latex:/img1db768b089db92fc4c4f71db7190d79b.png) . Show that if
. Show that if  is non-empty, then there exists
is non-empty, then there exists ![Math $a \in [U]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgeaef5363a091dd62e035800b50cebf97.png) such that for all
such that for all ![Math $b \in [U]$](/w/lib/exe/fetch.php?media=wiki:latex:/img95f2601817e30bb8f4c7d696f4d82d28.png) , we have
, we have ![Math $(a,b) \in [r]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgd15646db7eb5881fec12773862187e22.png) (that is,
(that is,  is the least element of
is the least element of ![Math $[U]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgb6999297622ced4acf55cc2b7b1d9e03.png) with respect to
with respect to ![Math $[r]$](/w/lib/exe/fetch.php?media=wiki:latex:/img8805783f428d9eceffcca44a82729afd.png) defined as in Problem 2).
defined as in Problem 2).